
【题目】已知△ABC中,AB=AC,BE平分∠ABC交边AC于E.
(1)如图(1),当∠BAC=108°时,证明:BC=AB+CE;
(2)如图(2),当∠BAC=100°时,(1)中的结论还成立吗?若不成立,是否有其他两条线段之和等于BC,若有请写出结论并完成证明.

【答案】(1)证明见解析;(2)BC=BE+AE,证明见解析.
【解析】
(1)如图1中,在BC上截取BD=BA.只要证明△BEA≌△BED,CE=CD即可解决问题;
(2)结论:BC=BE+AE.如图2中,在BA、BC上分别截取BF=BE,BH=BE.则△EBH≌△EBF,再证明EA=EH=EF=CF即可解决问题;
(1)如图1中,在BC上截取BD=BA.

∵BA=BD,∠EBA=∠EBD,BE=BE,
∴△BEA≌△BED,
∴BA=BD,∠A=∠BDE=108°,
∵AB=AC,
∴∠C=∠ABC=36°,∠EDC=72°,
∴∠CED=72°,
∴CE=CD,
∴BC=BD+CD=AB+CE.
(2)结论:BC=BE+AE.
理由:如图2中,在BA、BC上分别截取BF=BE,BH=BE.则△EBH≌△EBF,

∴EF=EH,
∵∠BAC=100°,AB=AC,
∴∠ABC=∠C=40°,
∴∠EBA=∠EBC=20°,
∴∠BFE=∠H=∠EAH=80°,
∴AE=EH,
∵∠BFE=∠C+∠FEC,
∴∠CEF=∠C=40°,
∴EF=CF,
∴BC=BF+CF=BE+AE.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是CD、BC上的点.若∠AEF=90°,则一定有( )
A.△ADE∽△ECF
B.△BCF∽△AEF
C.△ADE∽△AEF
D.△AEF∽△ABF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8cm,BC=16cm,点P从点A出发沿AB边想向点B以2cm/s的速度移动,点Q从点B出发沿BC边向点C以4cm/s的速度移动,如果P、Q同时出发,经过几秒后△PBQ和△ABC相似? 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG,DH分别与边AC,BC交于E,F两点.下列结论:①AE+BF=AC,②AE2+BF2=EF2,③S四边形CEDF=![]() S△ABC,④△DEF始终为等腰直角三角形.其中正确的是( )
S△ABC,④△DEF始终为等腰直角三角形.其中正确的是( )

A. ①②③④ B. ①②③ C. ①④ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件: , 可以使得△FDB与△ADE相似.(只需写出一个) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.

①李明同学做了如图乙的辅助线,将△BPC绕点B逆时针旋转60°,如图乙所示,连接PP′,从而问题得到解决.你能说明其中理由并完成问题解答吗?
②如图丙,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1;求∠BPC度数的大小和正方形ABCD的边长.
,PC=1;求∠BPC度数的大小和正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:O是坐标原点,P(m,n)(m>0)是函数y= ![]() (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+
(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+ ![]() .
.
(1)当n=1时,求点A的坐标;
(2)若OP=AP,求k的值;
(3)设n是小于20的整数,且k≠ ![]() ,求OP2的最小值.
,求OP2的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
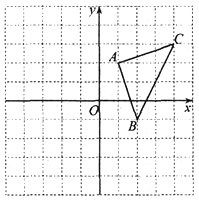
【题目】如图,平面直角坐标系中,△ABC的顶点坐标为:A(1,2),B(2, 一1), C (4, 3).
(1)将△ABC向左平移2个单位长度,再向上平移1个单位长度,得△A'B'C'.画出△A'B'C',并写出△A'B'C'的顶点坐标;
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com