
����Ŀ����ͼ�ף��ڵȱ�������ABC����һ��P����PA��2��PB��![]() ��PC��1�����BPC�����Ĵ�С�͵ȱ�������ABC�ı߳���
��PC��1�����BPC�����Ĵ�С�͵ȱ�������ABC�ı߳���

������ͬѧ������ͼ�ҵĸ����ߣ�����BPC�Ƶ�B��ʱ����ת60�㣬��ͼ����ʾ������PP�䣬�Ӷ�����õ����������˵���������ɲ������������
����ͼ������������ABCD����һ��P����PA��![]() ��BP��
��BP��![]() ��PC��1�����BPC�����Ĵ�С��������ABCD�ı߳���
��PC��1�����BPC�����Ĵ�С��������ABCD�ı߳���
���𰸡��ټ�����������BPC�Ķ�����135�㣬������ABCD�ı߳���![]() ��
��
��������
��������ת�ó�AP�䣽CP��1��BP�䣽BP��![]() ����AP��B����BPC�������ABP��+��ABP��60�㣬�õ��ȱߡ�BPP�䣬�Ƴ�PP�䣽PB��
����AP��B����BPC�������ABP��+��ABP��60�㣬�õ��ȱߡ�BPP�䣬�Ƴ�PP�䣽PB��![]() ����BP��P��60�㣬�����AP��P��90�㣬���������BPC������B��BM��AP�䣬��AP����ӳ����ڵ�M���ɡ�MP��B��30�㣬���BM��
����BP��P��60�㣬�����AP��P��90�㣬���������BPC������B��BM��AP�䣬��AP����ӳ����ڵ�M���ɡ�MP��B��30�㣬���BM��![]() ��P��M��
��P��M��![]() �����ݹ��ɶ�����������𰸣�
�����ݹ��ɶ�����������𰸣�
��ͬ�������BEP��![]() ��180�㩁90�㣩��45�㣬���ݹ��ɶ������涨�������AEP��90�㣬�Ƴ���BPC����AEB��90��+45�㣽135�㣻����B��BF��AE����AE���ӳ����ڵ�F�����FE��BF��1��AF��2�����ݹ��ɶ����������AB��
��180�㩁90�㣩��45�㣬���ݹ��ɶ������涨�������AEP��90�㣬�Ƴ���BPC����AEB��90��+45�㣽135�㣻����B��BF��AE����AE���ӳ����ڵ�F�����FE��BF��1��AF��2�����ݹ��ɶ����������AB��
�١ߡ�ABC�ǵȱ������Σ�
���ABC��60�㣬
����BPC�Ƶ�B��ʱ����ת60�㣬��ͼ����ʾ������PP�䣬
��AP�䣽CP��1��BP�䣽BP��![]() ����AP��B����BPC��
����AP��B����BPC��
����ת�ã���P'BP����ABC��60�㣬
���BPP���ǵȱ������Σ�
��PP�䣽PB��![]() ����BP��P��60�㣬
����BP��P��60�㣬
��AP�䣽1��AP��2��
��AP��2+PP��2��AP2��
���AP��P��90�㣬
���BPC����AP��B��90��+60�㣽150�㣬
����B��BM��AP�䣬��AP����ӳ����ڵ�M��
���MP��B��30�㣬BM��![]() P'B��
P'B��![]() ��
��
�ɹ��ɶ����ã�P��M��![]() ��
��![]() ��
��
��AM��AP'+P'M��1+![]() ��
��![]() ��
��
�ɹ��ɶ����ã�AB��![]() ��
��![]() ��
��![]() ��
��
�ڽ���BPC�Ƶ�B��ʱ����ת90��õ���AEB����ͼ����
��(1)���ƣ��ɵã�AE��PC��1��BE��BP��![]() ����BPC����AEB��
����BPC����AEB��
���EBP����ABC��90�㣬
���BEP��45�㣬
�ɹ��ɶ����ã�EP��2��
��AE��1��AP��![]() ��EP��2��
��EP��2��
��AE2+PE2��AP2��
���AEP��90�㣬
���BPC����AEB��90��+45�㣽135�㣬
����B��BF��AE����AE���ӳ����ڵ�F��
���FEB��45�㣬
��FE��BF��1��
��AF��2��
����Rt��ABF�У��ɹ��ɶ�������AB��![]() ��
��![]() ��
��
�𣺡�BPC�Ķ�����135�㣬������ABCD�ı߳���![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��ѧ��ȤС���ͬѧ���ñ�˲�����ˣ�AB���ĸ߶ȣ���һ��5�ߵı�ˣ�EF������ijһλ�ã���һ��ͬѧվ��һ�����ˡ���˳�һ��ֱ�ߣ���ʱ��������˶�������˶����غϣ�����һ��ͬѧ���վ����ͬѧ����3�ף������30�ף����վ����ͬѧ���۾�����棨CD��1.6�ף�����˵ĸ߶ȣ� 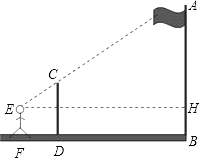
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������ABC�У���D��E�ֱ��ڱ�AC��AB�ϣ�AG��BC�ڵ�G��AF��DE�ڵ�F����EAF=��GAC��
��1����֤����ADE�ס�ABC��
��2����AD=3��AB=5���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ҫ�������и��⣺
(1)����![]() ��
��
(2)���ʽ���̣�![]() ��
��
(3)��֪����x�ķ���![]() ��һ�������⣬��m��ȡֵ��Χ��
��һ�������⣬��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�У�AB��AC��BEƽ�֡�ABC����AC��E��
(1)��ͼ(1)������BAC��108��ʱ��֤����BC��AB+CE��
(2)��ͼ(2)������BAC��100��ʱ��(1)�еĽ��ۻ������������������Ƿ������������߶�֮�͵���BC��������д�����۲����֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���D�DZ�AB���ĵȷֵ㣬DE��AC��DF��BC��AC=8��BC=12�����ı���DECF���ܳ��� 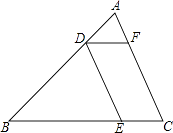
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������У�ij����ʳ��Ϊ�˱�֤�����ʳ�İ�ȫ���������ס��������ֿ����ʳ��ȫ��ת�Ƶ����н�ǿ�����ܵ�A��B���ֿ⣮��֪������ʳ100�֣��ҿ�����ʳ80�֣���A�������Ϊ70�֣�B�������Ϊ110�֣��Ӽס������A��B�����·�̺��˷����±��������С�Ԫ/��ǧ�ס���ʾÿ����ʳ����1ǧ����������ң�
·�̣�ǧ�ף� | �˷ѣ�Ԫ/��ǧ�ף� | |||
�� | �ҿ� | �� | �ҿ� | |
A�� | 20 | 15 | 12 | 12 |
B�� | 25 | 20 | 10 | 8 |
��1����������A����ʳx�֣���д������ʳ����A��B��������˷�y��Ԫ����x���֣��ĺ�����ϵʽ��
��2�����ס������������A��B������ٶ���ʳʱ�����˷���ʡ����ʡ�����˷��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵�����10̨A�ͺ�20̨B�͵��Ե�����Ϊ4000Ԫ������20̨A�ͺ�10̨B�͵��Ե�����Ϊ3500Ԫ��
(1)��ÿ̨A�͵��Ժ�B�͵��Ե���������
(2)���̵�ƻ�һ�ι��������ͺŵĵ��Թ�50̨������A�͵��ԵĽ�����������14̨��B�͵�Ľ�����������A�͵��Ե�2������ô���̵��м��ֽ�������?���̳�����A�͡�B�͵��Ը�����̨������ʹ�������������?
(3)ʵ�ʽ���ʱ�����Ҷ�A�͵��Գ������µ�m (0<m<100)Ԫ�����̵걣�����ֵ��Ե��ۼ۲��䣬�������������Ϣ��(2)����������Ƴ�ʹ��50̨�����������������Ľ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
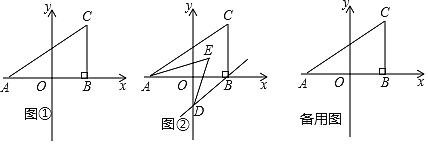
����Ŀ����ͼ�٣���ƽ��ֱ������ϵ�У�A![]() ��C
��C![]() ��������
��������![]() ����C��CB��
����C��CB��![]() ���ڵ�B.
���ڵ�B.
(1)![]()
(2)��![]() �����Ƿ���ڵ�P��ʹ��������ABC��������ACP�������ȣ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�����Ƿ���ڵ�P��ʹ��������ABC��������ACP�������ȣ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
(3)��ͼ�ڣ�������B��BD��AC��![]() ���ڵ�D����AE��DE�ֱ�ƽ�֡�CAB����ODB�����AED�Ķ���.
���ڵ�D����AE��DE�ֱ�ƽ�֡�CAB����ODB�����AED�Ķ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com