
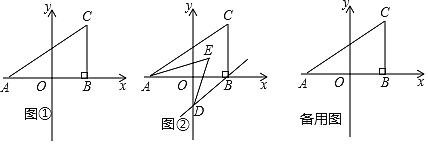
【题目】如图①,在平面直角坐标系中,A![]() ,C
,C![]() ,且满足
,且满足![]() 过点C作CB⊥
过点C作CB⊥![]() 轴于点B.
轴于点B.
(1)![]()
(2)在![]() 轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出点P的坐标;若不存在,请说明理由;
轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图②,若过点B作BD∥AC交![]() 轴于点D,且AE、DE分别平分∠CAB、∠ODB,求∠AED的度数.
轴于点D,且AE、DE分别平分∠CAB、∠ODB,求∠AED的度数.
【答案】(1)-2;2;4.(2)存在,P点坐标为(0,3),(0,-1).(3)∠AED =45°.
【解析】
(1)根据非负数的性质得a+2=0,b-2=0,解得a=-2,b=2,则A(-2,0),C(2,2),B(2,0),然后根据三角形面积公式计算S△ABC;
(2)如图③,AC交y轴于Q,先确定Q(0,1),设P(0,t),利用三角形面积公式和S△PAC=S△APQ+S△CPQ=S△ABC得到![]() |t-1|2+
|t-1|2+![]() |t-1|2=4,然后解方程求出t即可得到P点坐标;
|t-1|2=4,然后解方程求出t即可得到P点坐标;
(3)作EM∥AC,如图②,则AC∥EM∥BD,根据平行线的性质得∠CAE=∠AEM,∠BDE=∠DEM,则∠AED=∠CAE+∠BDE,而∠CAE=![]() ∠CAB,∠BDE=
∠CAB,∠BDE=![]() ∠ODB,所以∠AED=
∠ODB,所以∠AED=![]() (∠CAB+∠ODB),而由AC∥BD得到∠CAB=∠OBD,于是∠CAB+∠ODB=∠OBD+∠ODB=90°,则∠AED=45°.
(∠CAB+∠ODB),而由AC∥BD得到∠CAB=∠OBD,于是∠CAB+∠ODB=∠OBD+∠ODB=90°,则∠AED=45°.
解:(1)∵(a+2)2+![]() =0,
=0,
∴a+2=0,b-2=0,解得a=-2,b=2,
∴A(-2,0),C(2,2),
∵CB⊥x轴,
∴B(2,0),
∴S△ABC=![]() ×(2+2)×2=4;
×(2+2)×2=4;
故答案为:-2,2,4.
(2)存在.
如图③,AC交y轴于Q, 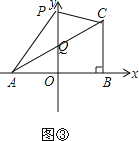
设Q点坐标为(0,y),依据S△ABC=S△AOQ+S梯形BOQC得:
![]() ,
,
解得y=1,即Q为(0,1)。
设P(0,t),
∵S△PAC=S△APQ+S△CPQ,S△PAC =S△ABC=4,
∴![]() |t-1|2+
|t-1|2+![]() |t-1|2=4,解得t=3或t=-1,
|t-1|2=4,解得t=3或t=-1,
∴P点坐标为(0,3),(0,-1);
(3)作EM∥AC,如图②,
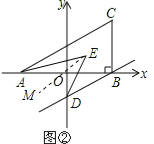
∵AC∥BD,
∴AC∥EM∥BD,
∴∠CAE=∠AEM,∠BDE=∠DEM,
∴∠AED=∠CAE+∠BDE,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠CAE=![]() ∠CAB,∠BDE=
∠CAB,∠BDE=![]() ∠ODB,
∠ODB,
∴∠AED=![]() (∠CAB+∠ODB),
(∠CAB+∠ODB),
∵AC∥BD,
∴∠CAB=∠OBD,
∴∠CAB+∠ODB=∠OBD+∠ODB=90°,
∴∠AED=![]() ×90°=45°.
×90°=45°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图甲,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.

①李明同学做了如图乙的辅助线,将△BPC绕点B逆时针旋转60°,如图乙所示,连接PP′,从而问题得到解决.你能说明其中理由并完成问题解答吗?
②如图丙,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1;求∠BPC度数的大小和正方形ABCD的边长.
,PC=1;求∠BPC度数的大小和正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:已知两直线,L1:y=k1x+b1,L2:y=k2x+b2,若L1⊥L2,则有k1k2=﹣1,根据以上结论解答下列各题:
(1)已知直线y=2x+1与直线y=kx﹣1垂直,求k的值.
(2)若一条直线经过A(2,3),且与y=![]() x+3垂直,求这条直线的函数关系式.
x+3垂直,求这条直线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在进行二次根式化简时,我们有时会碰上如![]() ,
,![]() ,
,![]() 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简:![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() =
=![]() -1,
-1,![]() 还可以用以下方法化简:
还可以用以下方法化简:![]() =
=![]() =
=![]() =
=![]() =
=![]() -1.以上这种化简的方法叫做分母有理化.(1)请化简
-1.以上这种化简的方法叫做分母有理化.(1)请化简![]() =________;(2)若a是
=________;(2)若a是![]() 的小数部分则
的小数部分则![]() =________;(3)矩形的面积为3
=________;(3)矩形的面积为3![]() +1,一边长为
+1,一边长为![]() -2,则它的周长为________;(4)化简
-2,则它的周长为________;(4)化简![]() +
+![]() +
+![]() +…+
+…+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
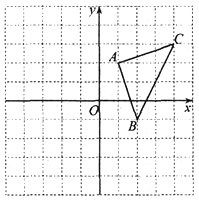
【题目】如图,平面直角坐标系中,△ABC的顶点坐标为:A(1,2),B(2, 一1), C (4, 3).
(1)将△ABC向左平移2个单位长度,再向上平移1个单位长度,得△A'B'C'.画出△A'B'C',并写出△A'B'C'的顶点坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE是线段AB的延长线,且∠CBE=∠A=∠C.
(1)由∠CBE=∠A可以判断____∥_____,根据是_____________;
(2)由∠CBE=∠C可以判断____∥_____,根据是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是平行四边形ABCD的AB边中点,CM交BD于点E,则图中阴影部分的面积与平行四边形ABCD的面积的比是( )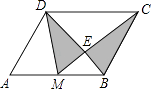
A.1:3
B.1:4
C.1:6
D.5:12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某山的山顶B处有一个观光塔,已知该山的山坡面与水平面的夹角∠BDC为30°,山高BC为100米,点E距山脚D处150米,在点E处测得观光塔顶端A的仰角为60°,则观光塔AB的高度是( )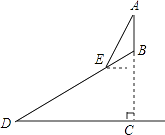
A.50米
B.100米
C.125米
D.150米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(1)直接写出一次函数y=kx+b的表达式和反比例函数y=![]() (x>0)的表达式;
(x>0)的表达式;
(2)求证:AD=BC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com