
【题目】如图,某数学兴趣小组的同学利用标杆测量旗杆(AB)的高度:将一根5米高的标杆(EF)竖在某一位置,有一名同学站在一处与标杆、旗杆成一条直线,此时他看到标杆顶端与旗杆顶端重合,另外一名同学测得站立的同学离标杆3米,离旗杆30米.如果站立的同学的眼睛距地面(CD)1.6米,求旗杆的高度. 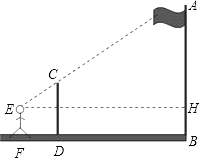
【答案】解:过点E作EH⊥AB于点H,交CD于点G. 由题意可得 四边形EFDG、GDHB都是矩形,AB∥CD∥EF.
∴△AECG∽△EAH.
∴ ![]() .
.
由题意可得
EG=FD=3,GH=BD=30,CG=CD﹣GD=CD﹣EF=5﹣1.6=3.4.
∴ ![]() .
.
∴AH=34米.
∴AH=AH+HB=34+1.6=35.6米.
答:旗杆高ED为35.6米.
【解析】过点E作CG⊥AH于点H,交CD于点G得出△EGC∽△EHA,进而求出AH的长,进而求出AB的长.
【考点精析】解答此题的关键在于理解相似三角形的应用的相关知识,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.


科目:初中数学 来源: 题型:
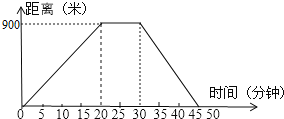
【题目】如图,反映了小明从家里到超市的时间与距离之间关系的一幅图。
(1)图中自变量和因变量各是什么?
(2)小明到达超市用了多少时间?超市离家多远?
(3)分别求小明从家里到超市时的平均速度是多少?返回时的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
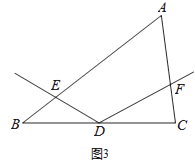
【题目】如图,在△ABC中,点D为BC边的任意一点,以点D为顶点的∠EDF的两边分别与边AB,AC交于点E、F,且∠EDF与∠A互补.
(1)如图1,若AB=AC,D为BC的中点时,则线段DE与DF有何数量关系?请直接写出结论;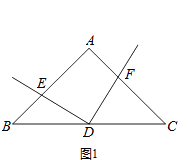
(2)如图2,若AB=kAC,D为BC的中点时,那么(1)中的结论是否还成立?若成立,请给出证明;若不成立,请写出DE与DF的关系并说明理由;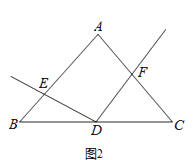
(3)如图3,若 ![]() =a,且
=a,且 ![]() =b,直接写出
=b,直接写出 ![]() = .
= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
A.13
B.14
C.15
D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是CD、BC上的点.若∠AEF=90°,则一定有( )
A.△ADE∽△ECF
B.△BCF∽△AEF
C.△ADE∽△AEF
D.△AEF∽△ABF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形纸片ABC中,点D在边AB(不包含端点A、B)上运动,连接CD,将∠ADC对折,点A落在直线CD上的点A′处,得到折痕DE;将∠BDC对折,点B落在直线CD上的点B′处,得到折痕DF.
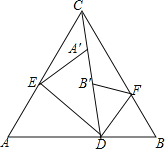
(1)若∠ADC=80°,求∠BDF的度数;
(2)试问∠EDF的大小是否会随着点D的运动而变化?若不变,求出∠EDF的大小;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC与BD交于点O,下列各组条件,其中不能判定四边形ABCD是平行四边形的是( )
A. OA=OC,OB=ODB. OA=OC,AB∥CD
C. AB=CD,OA=OCD. ∠ADB=∠CBD,∠BAD=∠BCD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2018年西安女子半程马拉松”的赛事有两项:A“女子半程马拉松”;B、“5公里女子健康跑”.小明对部分参赛选手作了如下调查:
调查总人数 | 50 | 100 | 200 | 300 | 400 | 500 |
参加“5公里女子健康跑”人数 | 18 | 45 | 79 | 120 | 160 | b |
参加“5公里女子健康跑”频率 | 0.360 | a | 0.395 | 0.400 | 0.400 | 0.400 |

(1)计算表中a,b的值;
(2)在图中,画出参赛选手参加“5公里女子健康跑“的频率的折线统计图;
(3)从参赛选手中任选一人,估计该参赛选手参加“5公里女子健康跑”的概率(精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.

①李明同学做了如图乙的辅助线,将△BPC绕点B逆时针旋转60°,如图乙所示,连接PP′,从而问题得到解决.你能说明其中理由并完成问题解答吗?
②如图丙,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1;求∠BPC度数的大小和正方形ABCD的边长.
,PC=1;求∠BPC度数的大小和正方形ABCD的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com