
【题目】如图,在△ABC中,点D为BC边的任意一点,以点D为顶点的∠EDF的两边分别与边AB,AC交于点E、F,且∠EDF与∠A互补.
(1)如图1,若AB=AC,D为BC的中点时,则线段DE与DF有何数量关系?请直接写出结论;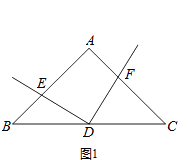
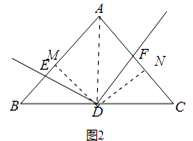
(2)如图2,若AB=kAC,D为BC的中点时,那么(1)中的结论是否还成立?若成立,请给出证明;若不成立,请写出DE与DF的关系并说明理由;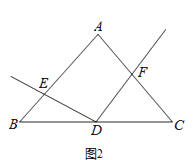
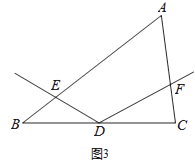
(3)如图3,若 ![]() =a,且
=a,且 ![]() =b,直接写出
=b,直接写出 ![]() = .
= . 
【答案】
(1)解:结论:DF=DE,
理由:如图1,连接AD,作DM⊥AB于M,DN⊥AC于N,则∠EMD=∠FND=90°,
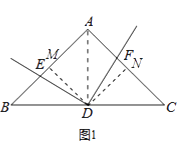
∵AB=AC,点D为BC中点,
∴AD平分∠BAC,
∴DM=DN,
∵在四边形AMDN中.,∠DMA=∠DNA=90°,
∴∠MAN+∠MDN=180°,
又∵∠EDF与∠MAN互补,
∴∠MDN=∠EDF,
∴∠EDM=∠FDN,
在△DEM与△DFN中,
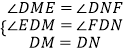 ,
,
∴△DEM≌△DFN,
∴DE=DF.
(2)解:结论DE:DF=1:k.
理由:如图2,过点D作DM⊥AB于M,作DN⊥AC于N,连接AD,则∠EMD=∠FND=90°,
∵BD=DC,
∴S△ABD=S△ADC,
∴ ![]() ABDM=
ABDM= ![]() ACDN,∵AB=kAC,
ACDN,∵AB=kAC,
∴DN=kDM,
由(2)可知,∠EDM=∠FDN,∠DEM=∠DFN=90°,
∴△DME∽△DNF,
∴ ![]() =
= ![]() =
= ![]() .
.
(3)![]()
【解析】(3)结论: ![]() =
= ![]() .
.
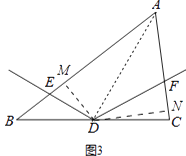
理由:如图3,过点D作DM⊥AB于M,作DN⊥AC于N,连接AD,同(2)可证∠EDM=∠FDN,
又∵∠EMD=∠FND=90°,
∴△DEM∽△DFN,
∴ ![]() =
= ![]() ,
,
∵ ![]() =b,
=b,
∴S△ABD:S△ADC=b,
∴ ![]() ABDM:
ABDM: ![]() ACDN=b,∵AB:AC=a,
ACDN=b,∵AB:AC=a,
∴DM:DN= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() .
.
所以答案是 ![]() .
.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】南博汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价x万元,每辆汽车的销售利润为y万元.(销售利润=销售价﹣进货价)
(1)求y与x的函数关系式;在保证商家不亏本的前提下,写出x的取值范围;
(2)假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2.
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形纸片ABCD沿EF折叠后,ED与BC交点为G,D、C分别在M、N的位置上,若∠2-∠1=40°,则∠EFC的度数为( )
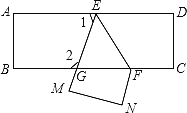
A. 115°B. 125°C. 135°D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.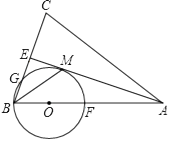
(1)求证:AE为⊙O的切线;
(2)当BC=4,AC=6时,求⊙O的半径;
(3)在(2)的条件下,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组的同学利用标杆测量旗杆(AB)的高度:将一根5米高的标杆(EF)竖在某一位置,有一名同学站在一处与标杆、旗杆成一条直线,此时他看到标杆顶端与旗杆顶端重合,另外一名同学测得站立的同学离标杆3米,离旗杆30米.如果站立的同学的眼睛距地面(CD)1.6米,求旗杆的高度. 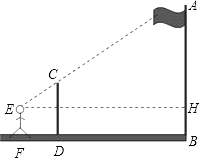
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com