
【题目】如图,在半径为 ![]() 的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为( )
的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为( )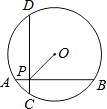
A.1
B.![]()
C.2
D.2 ![]()
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
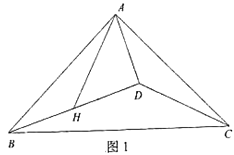
【题目】已知等腰Rt△ABC,∠BAC=90°,AB=AC,点D为△ABC内部一点,连接AD、BD、CD,点H为BD中点,连接AH,且∠BAH=∠ACD.
(1)如图1,若∠ADB=90°,求证:∠DAH=45°;
(2)如图2,若∠ADB<90°,(1)问中的结论是否成立,若成立,请证明;若不成立,请说明理由.
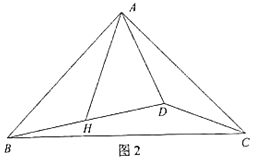
查看答案和解析>>
科目:初中数学 来源: 题型:
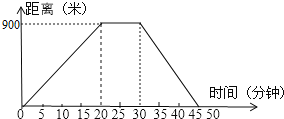
【题目】如图,反映了小明从家里到超市的时间与距离之间关系的一幅图。
(1)图中自变量和因变量各是什么?
(2)小明到达超市用了多少时间?超市离家多远?
(3)分别求小明从家里到超市时的平均速度是多少?返回时的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),将直线y=kx沿y轴向上平移3个单位长度后恰好经过B,C两点.
(1)求直线BC及抛物线的解析式;
(2)设抛物线的顶点为D,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标;
(3)连接CD,求∠OCA与∠OCD两角和的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个.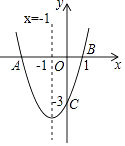
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三角形的两边分别是2cm和3cm,现从长度分别为1cm、2cm、3cm、4cm、5cm、6cm六根小木棒中随机抽一根,抽到的木棒能作为该三角形第三边的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
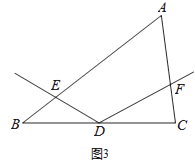
【题目】如图,在△ABC中,点D为BC边的任意一点,以点D为顶点的∠EDF的两边分别与边AB,AC交于点E、F,且∠EDF与∠A互补.
(1)如图1,若AB=AC,D为BC的中点时,则线段DE与DF有何数量关系?请直接写出结论;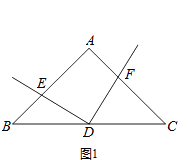
(2)如图2,若AB=kAC,D为BC的中点时,那么(1)中的结论是否还成立?若成立,请给出证明;若不成立,请写出DE与DF的关系并说明理由;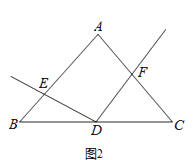
(3)如图3,若 ![]() =a,且
=a,且 ![]() =b,直接写出
=b,直接写出 ![]() = .
= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
A.13
B.14
C.15
D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2018年西安女子半程马拉松”的赛事有两项:A“女子半程马拉松”;B、“5公里女子健康跑”.小明对部分参赛选手作了如下调查:
调查总人数 | 50 | 100 | 200 | 300 | 400 | 500 |
参加“5公里女子健康跑”人数 | 18 | 45 | 79 | 120 | 160 | b |
参加“5公里女子健康跑”频率 | 0.360 | a | 0.395 | 0.400 | 0.400 | 0.400 |

(1)计算表中a,b的值;
(2)在图中,画出参赛选手参加“5公里女子健康跑“的频率的折线统计图;
(3)从参赛选手中任选一人,估计该参赛选手参加“5公里女子健康跑”的概率(精确到0.1).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com