
【题目】已知等腰Rt△ABC,∠BAC=90°,AB=AC,点D为△ABC内部一点,连接AD、BD、CD,点H为BD中点,连接AH,且∠BAH=∠ACD.
(1)如图1,若∠ADB=90°,求证:∠DAH=45°;
(2)如图2,若∠ADB<90°,(1)问中的结论是否成立,若成立,请证明;若不成立,请说明理由.
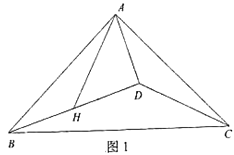
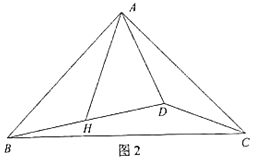
【答案】(1)证明见解析;(2)成立.
【解析】
(1)用ASA证明△ABH≌△CAD,得到BH=AD,即AD=HD,得到△AHD是等腰直角三角形,即可得出结论;
(2)延长AH到E,使HE=AH,连接DE.延长CD交AB于F,交AH于G.通过证明△ABH≌△EDH和△EGD≌△CGA,得到△AGD为等腰直角三角形,即可得出结论.
(1)∵∠BAC=90°,∴∠CAD+∠BAD=90°.
∵∠ADB=90°,∴∠ABH+∠BAD=90°,∴∠CAD=∠ABH.
在△ABH和△CAD中,∵∠BAH=∠ACD,AB=CA,∠ABH=∠CAD,∴△ABH≌△CAD(ASA),∴BH=AD.
∵H为BD的中点,∴BH=HD,∴AD=HD,∴△AHD是等腰直角三角形,∴∠DAH=45°.
(2)成立.理由如下:
如图,延长AH到E,使HE=AH,连接DE.延长CD交AB于F,交AH于G.
∵BH=DH,∠BHA=∠DHE,AH=EH,∴△ABH≌△EDH,∴AB=ED,∠1=∠E.
∵AB=AC,∴ED=AC.
∵∠1=∠2,∴∠E=∠2.
∵∠BAC=90°,∴∠1+∠GAC=90°.
∵∠1=∠2,∴∠2+∠GAC=90°,∴∠AGC=90°,∴∠EGD=∠CGA=90°.
在△EGD和△CGA中,∵∠E=∠2,∠EGD=∠CGA,ED=CA,∴△EGD≌△CGA(AAS),∴GD=GA,∴△AGD为等腰直角三角形,∴∠DAH=45°.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】某调查小组采用简单随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样调查,并把所得数据整理后绘制成如下的统计图: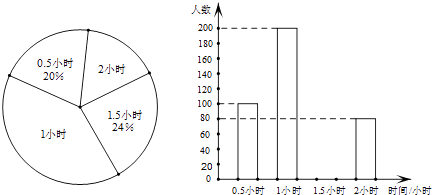
(1)该调查小组抽取的样本容量是多少?
(2)求样本学生中阳光体育运动时间为1.5小时的人数,并补全占频数分布直方图;
(3)请估计该市中小学生一天中阳光体育运动的平均时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,c为斜边,a、b为直角边,则化简 ![]() 的结果为( )
的结果为( )
A.3a+b﹣c
B.﹣a﹣3b+3c
C.a+3b﹣3c
D.2a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商店经销一种苹果,共有20筐,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如表:
与标准质量的差值(单位;千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)这20筐苹果中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,这20筐苹果总计超过或不足多少千克?
(3)若苹果每千克售价![]() 元,则出售这20筐苹果可卖多少元?
元,则出售这20筐苹果可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:小明遇到这样一个问题:
如图1,在△ABC中,∠B=2∠C,AD⊥BC于点D,求证:BC=AB+2BD.
小明利用条件AD⊥BC,在CD上截取DH=BD,如图2,连接AH,既构造了等腰△ABH,又得到BH=2BD,从而命题得证。
(1)根据阅读材料,证明:BC=AB+2BD;
(2)参考小明的方法,解决下面的问题:
如图3,在△ABC中,∠BAC=90°,∠ABD=∠BCE,∠ABC=∠DCE,请探究AD与BE的数量关系,并说明理由。

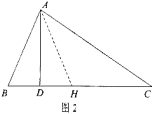

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,则△ADE周长是多少?为什么?
(2)若∠BAC=128°,则∠DAE的度数是多少?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1 ,
(2)点C1的坐标是;
(3)以点B为位似中心,在网格内画出△A2B2C2 ,
(4)使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com