
【题目】阅读下面材料:小明遇到这样一个问题:
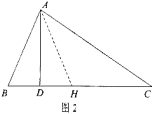
如图1,在△ABC中,∠B=2∠C,AD⊥BC于点D,求证:BC=AB+2BD.
小明利用条件AD⊥BC,在CD上截取DH=BD,如图2,连接AH,既构造了等腰△ABH,又得到BH=2BD,从而命题得证。
(1)根据阅读材料,证明:BC=AB+2BD;
(2)参考小明的方法,解决下面的问题:
如图3,在△ABC中,∠BAC=90°,∠ABD=∠BCE,∠ABC=∠DCE,请探究AD与BE的数量关系,并说明理由。


【答案】(1)证明见解析;(2)BE=2AD.
【解析】
(1)由BD=DH,AD⊥BH,得到AB=AH,由等边对等角得到∠B=∠AHB,再由∠B=2∠C和三角形外角的性质得到∠C=∠CAH,由等角对等边得到AH=HC,即有AB=HC,从而可以得出结论;
(2)延长DA至点F,使得AF=AD,连接BF.设∠ABD=∠BCE=x,∠ABC=∠DCE=y.
证明BA垂直平分DF,得到BF=BD,∠1=∠DBA=x,进而得到∠FBC=∠ACB,由等角对等边得到BF=CF,即有BD=FC.由三角形外角的性质得到∠2=∠DCE,则有DE=DC,结合BD=CF,即可得到结论.
(1)∵BD=DH,AD⊥BH,∴AB=AH,∴∠B=∠AHB.
∵∠B=2∠C,∴∠AHB=2∠C=∠C+∠CAH,∴∠C=∠CAH,∴AH=HC,∴AB=HC,∴BC=HC+BH=AB+2BD.
(2)BE=2AD.理由如下:
延长DA至点F,使得AF=AD,连接BF.设∠ABD=∠BCE=x,∠ABC=∠DCE=y.
∵AF=AD,∠BAD=90°,∴BA垂直平分DF,∴BF=BD,∠1=∠DBA=x,∴∠FBC=∠1+∠ABC=x+y,∠ACB=∠DCE+∠ECB=x+y,∴∠FBC=∠ACB,∴BF=CF.
∵BF=BD,∴BD=FC.
∵∠2=∠3+x=∠ABC=y=∠DCE,∴DE=DC.
∵BD=FC,∴BE+DE=2AD+DC,∴BE=2AD.


 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】有一直角三角形纸片,∠C=90°,BC=6,AC=8,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长为( )
A. 2![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将一幅三角板按如图所示的方式放置,则下列结论中不正确的是( )

A. ∠1=∠3 B. 如果∠2=30°,则有AC∥DE
C. 如果∠2=30°,则有BC∥AD D. 如果∠2=30°,必有∠4=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学期结束前,学校想调查七年级学生对新课改实验教材的意见,特向七年级480名学生作了问卷调查,结果如下表所示:
意见 | 非常喜欢 | 喜欢 | 有一点喜欢 | 不喜欢 |
人数 | 240 | 192 | 44 | 4 |
(1)计算出每一种意见的人数占调查总人数的百分比;
(2)请作出反映此调查结果的扇形统计图;
(3)从统计图中你能得出什么结论?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
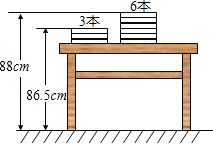
【题目】如图,两摞规格完全相同的课本整齐叠放在讲台上请根据图中所给出的数据信息,回答下列问题:
(1)每本课本的厚度为______cm;
(2)若有一摞上述规格的课本x本,整齐叠放在讲台上,请用含x的代数式表示出这一摞数学课本的顶部距离地面的高度为______cm;
(3)当x=48时,若从中取走10本,求余下的课本的顶部距离地面的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰Rt△ABC,∠BAC=90°,AB=AC,点D为△ABC内部一点,连接AD、BD、CD,点H为BD中点,连接AH,且∠BAH=∠ACD.
(1)如图1,若∠ADB=90°,求证:∠DAH=45°;
(2)如图2,若∠ADB<90°,(1)问中的结论是否成立,若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点A(6,0),又点B(x,y)在第一象限内,且x+y=8,设△AOB的面积是S.
(1)写出S与x之间的函数解析式,并求出x的取值范围;
(2)画出(1)中所求函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
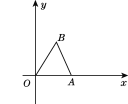
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF.
(2)若连接AD、CF,则这两条线段之间的关系是 .
(3)画出△ABC的BC边上的高AM。
(4)满足三角形ACP的面积等于三角形ACB的面积的格点P有 个(不和B重合)
查看答案和解析>>
科目:初中数学 来源: 题型:
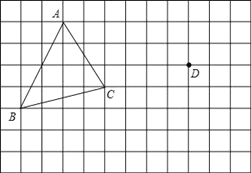
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com