
【题目】有一直角三角形纸片,∠C=90°,BC=6,AC=8,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长为( )
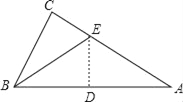
A. 2![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4
科目:初中数学 来源: 题型:
【题目】(10分)如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.

(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,M是边AB的中点,CH⊥AB于点H,CD平分∠ACB.

(1)求证:∠1=∠2.
(2)过点M作AB的垂线交CD的延长线于点E,连结AE,BE.求证:CM=EM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大华服装厂生产一件秋冬季外套需面料1.2米,里料0.8米,已知面料的单价比里料的单价的2倍还多10元,一件外套的布料成本为76元.
(1)求面料和里料的单价;
(2)该款外套9月份投放市场的批发价为150元/件,出现购销两旺态势,10月份进入批发淡季,厂方决定采取打折促销.已知生产一件外套需人工等固定费用14元,为确保每件外套的利润不低于30元.
①设10月份厂方的打折数为m,求m的最小值;(利润=销售价﹣布料成本﹣固定费用)
②进入11月份以后,销售情况出现好转,厂方决定对VIP客户在10月份最低折扣价的基础上实施更大的优惠,对普通客户在10月份最低折扣价的基础上实施价格上浮.已知对VIP客户的降价率和对普通客户的提价率相等,结果一个VIP客户用9120元批发外套的件数和一个普通客户用10080元批发外套的件数相同,求VIP客户享受的降价率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某营业厅对手机话费业务有如下的优惠:
优惠规则:
①用户手机账户原有话费不能低于240元;
②办理业务时,首先从手机账户中一次性扣除240元,并把这240元抵为300元话费,然后将这300元话费分12次,在每月的15号等额返还到手机账户;
③每月1号从手机账户中扣除话费49元,当月不再扣除其他任何费用;
④每月1号手机账户的话费余额不足以扣除49元时,视为欠费,则当月不再返还等额的话费.
小明的手机账户中原有话费400元,办理了这项优惠业务,设小明的手机账户中每个月末的话费余额是y(元),月数为x(个),则
(1)每个月等额返还的话费是元,第2个月末的话费余额是元;
(2)求y关于x的函数关系式;
(3)若不续费,小明的手机第几个月会欠费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某调查小组采用简单随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样调查,并把所得数据整理后绘制成如下的统计图: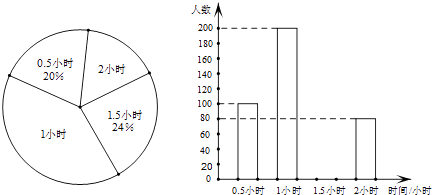
(1)该调查小组抽取的样本容量是多少?
(2)求样本学生中阳光体育运动时间为1.5小时的人数,并补全占频数分布直方图;
(3)请估计该市中小学生一天中阳光体育运动的平均时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数。
解:∵EF∥AD,
∴∠2= ( )
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=70°,∴∠AGD= 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在五一期间组织学生外出旅游,如果单独租用45座的客车若干辆,恰好坐满;如果单独租用60座的客车,可少租一辆,并且余30个座位.
(1)求外出旅游的学生人数是多少,单租45座的客车需多少辆?
(2)已知45座的客车每辆租金250元,60座的客车每辆租金300元,为节省租金,并且保证每个学生都有座,决定同时租用两种客车,使得租车总数比单租45座的客车少一辆,问45座的客车和60座的客车分别租多少辆才能使得租金最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:小明遇到这样一个问题:
如图1,在△ABC中,∠B=2∠C,AD⊥BC于点D,求证:BC=AB+2BD.
小明利用条件AD⊥BC,在CD上截取DH=BD,如图2,连接AH,既构造了等腰△ABH,又得到BH=2BD,从而命题得证。
(1)根据阅读材料,证明:BC=AB+2BD;
(2)参考小明的方法,解决下面的问题:
如图3,在△ABC中,∠BAC=90°,∠ABD=∠BCE,∠ABC=∠DCE,请探究AD与BE的数量关系,并说明理由。

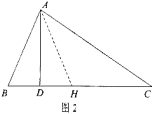

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com