
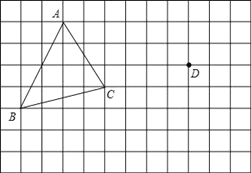
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF.
(2)若连接AD、CF,则这两条线段之间的关系是 .
(3)画出△ABC的BC边上的高AM。
(4)满足三角形ACP的面积等于三角形ACB的面积的格点P有 个(不和B重合)
【答案】(1)详见解析;(2)平行且相等;(3)详见解析;(4)4.
【解析】
(1)根据网格结构找出点B、C平移后的对应点E、F的位置,然后与点D顺次连接即可;
(2)根据平移的性质,对应点的连线平行且相等;
(3)根据网格结构和三角形的高线的定义作出图形即可;
(4)过B作AC的平行线,过D作AC的平行线,即可得出格点P有4个.
(1) 如图:
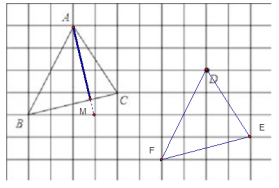
(2)根据平移的性质,对应点的连线平行且相等平行且相等;
(3)根据网格结构和三角形的高线的定义作出图形,如图:
(4)
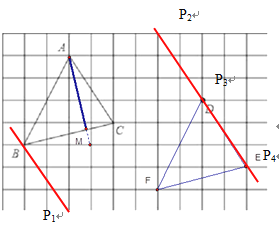
如图,过B作AC的平行线,过D作AC的平行线,
当点P在点P1,点P2,点P3,点P4处时,存在S△ACB=S△ACP,
∴格点P有4个.
故答案为:4.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】某校在五一期间组织学生外出旅游,如果单独租用45座的客车若干辆,恰好坐满;如果单独租用60座的客车,可少租一辆,并且余30个座位.
(1)求外出旅游的学生人数是多少,单租45座的客车需多少辆?
(2)已知45座的客车每辆租金250元,60座的客车每辆租金300元,为节省租金,并且保证每个学生都有座,决定同时租用两种客车,使得租车总数比单租45座的客车少一辆,问45座的客车和60座的客车分别租多少辆才能使得租金最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:小明遇到这样一个问题:
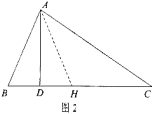
如图1,在△ABC中,∠B=2∠C,AD⊥BC于点D,求证:BC=AB+2BD.
小明利用条件AD⊥BC,在CD上截取DH=BD,如图2,连接AH,既构造了等腰△ABH,又得到BH=2BD,从而命题得证。
(1)根据阅读材料,证明:BC=AB+2BD;
(2)参考小明的方法,解决下面的问题:
如图3,在△ABC中,∠BAC=90°,∠ABD=∠BCE,∠ABC=∠DCE,请探究AD与BE的数量关系,并说明理由。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1 ,
(2)点C1的坐标是;
(3)以点B为位似中心,在网格内画出△A2B2C2 ,
(4)使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地而上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1: ![]() ,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:
,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1: ![]() 是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取
是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取 ![]() =1.732,结果精确到0.1m).
=1.732,结果精确到0.1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南博汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价x万元,每辆汽车的销售利润为y万元.(销售利润=销售价﹣进货价)
(1)求y与x的函数关系式;在保证商家不亏本的前提下,写出x的取值范围;
(2)假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.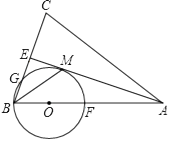
(1)求证:AE为⊙O的切线;
(2)当BC=4,AC=6时,求⊙O的半径;
(3)在(2)的条件下,求线段BG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com