
【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),将直线y=kx沿y轴向上平移3个单位长度后恰好经过B,C两点.
(1)求直线BC及抛物线的解析式;
(2)设抛物线的顶点为D,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标;
(3)连接CD,求∠OCA与∠OCD两角和的度数.
【答案】
(1)解:∵y=kx沿y轴向上平移3个单位长度后经过y轴上的点C, 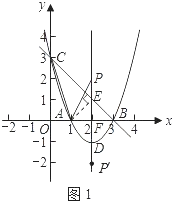
∴C(0,3).
设直线BC的解析式为y=kx+3.
∵B(3,0)在直线BC上,
∴3k+3=0.
解得k=﹣1.
∴直线BC的解析式为y=﹣x+3.
∵抛物线y=x2+bx+c过点B,C,
∴ ![]()
解得 ![]() ,
,
∴抛物线的解析式为y=x2﹣4x+3.
(2)解:由y=x2﹣4x+3.
可得D(2,﹣1),A(1,0).
∴OB=3,OC=3,OA=1,AB=2.
可得△OBC是等腰直角三角形,
∴∠OBC=45°,CB=3 ![]() .
.
如图1,设抛物线对称轴与x轴交于点F,
∴AF= ![]() AB=1.
AB=1.
过点A作AE⊥BC于点E.
∴∠AEB=90度.
可得BE=AE= ![]() ,CE=2
,CE=2 ![]() .
.
在△AEC与△AFP中,∠AEC=∠AFP=90°,∠ACE=∠APF,
∴△AEC∽△AFP.
∴ ![]() ,
, ![]() .
.
解得PF=2.∵点P在抛物线的对称轴上,
∴点P的坐标为(2,2)或(2,﹣2).
(3)解:解法一:
如图2, 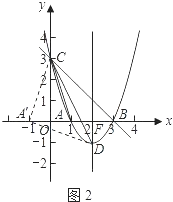
作点A(1,0)关于y轴的对称点A',则A'(﹣1,0).
连接A'C,A'D,
可得A'C=AC= ![]() ,∠OCA'=∠OCA.
,∠OCA'=∠OCA.
由勾股定理可得CD2=20,A'D2=10.
又∵A'C2=10,
∴A'D2+A'C2=CD2.
∴△A'DC是等腰直角三角形,∠CA'D=90°,
∴∠DCA'=45度.
∴∠OCA'+∠OCD=45度.
∴∠OCA+∠OCD=45度.
即∠OCA与∠OCD两角和的度数为45度.
解法二:
如图3,连接BD. 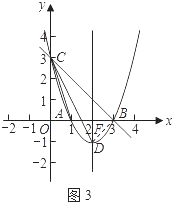
同解法一可得CD= ![]() ,AC=
,AC= ![]() .
.
在Rt△DBF中,∠DFB=90°,BF=DF=1,
∴DB= ![]() .
.
在△CBD和△COA中, ![]() ,
, ![]() ,
, ![]() .
.
∴ ![]() .
.
∴△CBD∽△COA.
∴∠BCD=∠OCA.
∵∠OCB=45°,
∴∠OCA+∠OCD=45度.
即∠OCA与∠OCD两角和的度数为45度.
【解析】直线y=kx向上平移3个单位与y轴交于C,可知C(0,3)代入抛物线解析式即可求出b、c;(2)由∠APD=∠ACB可构造△AEC∽△AFP,由对应边成比例可求出PF,进而求出P坐标;(3)求两角和可转化某一个角然后这两者再相加组成一个角,可由△CBD∽△COA可得出 ∠BCD=∠OCA,∠OCA+∠OCD=∠BCD=45度.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某水果商店经销一种苹果,共有20筐,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如表:
与标准质量的差值(单位;千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)这20筐苹果中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,这20筐苹果总计超过或不足多少千克?
(3)若苹果每千克售价![]() 元,则出售这20筐苹果可卖多少元?
元,则出售这20筐苹果可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1 ,
(2)点C1的坐标是;
(3)以点B为位似中心,在网格内画出△A2B2C2 ,
(4)使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
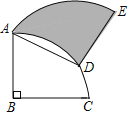
【题目】如图,将半径为4,圆心角为90°的扇形BAC绕A点逆时针旋转60°,点B、C的对应点分别为点D、E且点D刚好在![]() 上,则阴影部分的面积为_____.
上,则阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南博汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价x万元,每辆汽车的销售利润为y万元.(销售利润=销售价﹣进货价)
(1)求y与x的函数关系式;在保证商家不亏本的前提下,写出x的取值范围;
(2)假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】曲靖市某商场投入19200元资金购进甲、乙两种饮料共600箱,饮料的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 36 | 52 |
(1)该商场购进甲、乙两种饮料各多少箱?
(2)全部售完600箱饮料,该商场共获得利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形纸片ABCD沿EF折叠后,ED与BC交点为G,D、C分别在M、N的位置上,若∠2-∠1=40°,则∠EFC的度数为( )
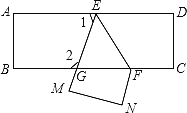
A. 115°B. 125°C. 135°D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好.
(1)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;
(2)琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2 , 并指出她与嘉嘉抽到勾股数的可能性一样吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com