
【题目】当![]() 时,
时,![]() ,则
,则![]() 的取值范围是_______.
的取值范围是_______.
【答案】m≥1
【解析】
设函数![]() ,令y=0,求出x,根据函数图像可知:在
,令y=0,求出x,根据函数图像可知:在![]() 或
或![]() 时,函数图像在-3≤x≤0的区域内位于x轴下方,再分
时,函数图像在-3≤x≤0的区域内位于x轴下方,再分![]() 或
或![]() 两种情况分别求解,最后合并.
两种情况分别求解,最后合并.
解:设函数![]() ,
,
则该函数的图像为开口向下的抛物线,
令:![]() ,得:
,得:
![]() =
=![]() =
=![]() ,
,
![]() =
=![]() =
=![]() ,
,
可得![]() ,
,
∴函数![]() 与x轴的交点为:
与x轴的交点为:
(![]() ,0),(
,0),(![]() ,0),
,0),
由于-3≤x≤0时,
![]() ,即函数
,即函数![]() 的图像在-3≤x≤0时位于x轴下方,根据函数图像可知:在
的图像在-3≤x≤0时位于x轴下方,根据函数图像可知:在![]() 或
或![]() 时,函数图像在-3≤x≤0的区域内位于x轴下方,
时,函数图像在-3≤x≤0的区域内位于x轴下方,
因此有![]() 或
或![]() 两种情况,
两种情况,
当![]() 时,函数
时,函数![]() 的对称轴直线x=m大于
的对称轴直线x=m大于![]() ,即m>0,
,即m>0,
![]() ≥0,
≥0,
![]() ,
,
∵m>0,
∴![]() ,得:m≥1,
,得:m≥1,
当![]() 时,函数
时,函数![]() 的对称轴直线x=m小于
的对称轴直线x=m小于![]() ,即m<-3,
,即m<-3,
![]() ,
,
![]() ,
,
∵m<-3,
∴m+3<0,
∴-(m+3)≥![]() ,
,
两边平方得:![]() ,
,
∵m<-3,
∴不成立,
故m的取值范围是m≥1.
故答案为:m≥1.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
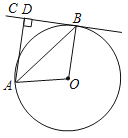
【题目】如图,AB是⊙O的弦,直线BC与⊙O相切于点B,AD⊥BC,垂足为D,连接OA,OB.
(1)求证:AB平分∠OAD;
(2)当∠AOB=100°,⊙O的半径为6cm时.
①直接写出扇形AOB的面积约为 cm2(结果精确到1cm2);
②点E是⊙O上一动点(点E不与点A、点B重合),连接AE,BE,请直接写出∠AEB= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为全面贯彻党的教育方针和落实阳光体育运动,提高青少年学生身体健康水平和体育运动水平,某校准备购买一批篮球,甲、乙两家商店的标价都是每个![]() 元,两家商店推出不同的优惠方式如下表:
元,两家商店推出不同的优惠方式如下表:
商店 | 优惠方式 |
甲 | 购买数量不超过 |
乙 | 按照标价的八折销售 |
(1)设该学校购买![]() 个篮球,在甲商店购买花费
个篮球,在甲商店购买花费![]() 元,在商店购买花费
元,在商店购买花费![]() 元,请分别求出
元,请分别求出![]() 、
、![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若学校需购买![]() 个篮球,请你通过计算进行对比,选择哪家商店更省钱?
个篮球,请你通过计算进行对比,选择哪家商店更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两种水稻实验品种连续5年的平均单位面积产量如下(单位:吨/公顷):
品种 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
甲 |
|
|
| 10 |
|
乙 |
|
|
|
|
|
(1)乙种水稻5年的平均单位面积产量的平均数为______吨/公顷;
(2)“扇形统计图”和“折线统计图”中,更能直观地反映甲种水稻5年的平均单位面积产量变化过程和趋势的统计图是______;
(3)王老汉家有100公顷田要种植水稻,你建议他种什么品种的水稻,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班班长统计去年18月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
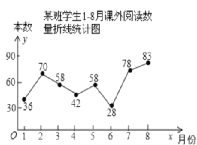
A. 每月阅读数量的平均数是50
B. 众数是42
C. 中位数是58
D. 每月阅读数量超过40的有4个月
查看答案和解析>>
科目:初中数学 来源: 题型:
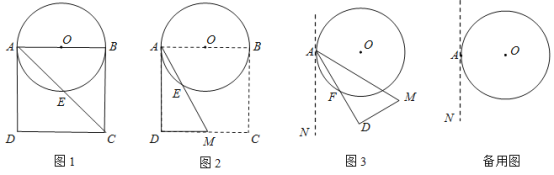
【题目】如图![]() , 以边长为
, 以边长为![]() 的正方形纸片
的正方形纸片![]() 的边
的边![]() 为直径做
为直径做![]() , 交对角线
, 交对角线![]() 于点
于点![]() .
.
(1)线段![]()
(2) 如图![]() , 以点
, 以点![]() 为端点作
为端点作![]() , 交
, 交![]() 于点
于点![]() , 沿
, 沿![]() 将四边形
将四边形![]() 剪掉, 使
剪掉, 使![]() 绕点
绕点![]() 逆时针旋转(如图
逆时针旋转(如图![]() ),设旋转角为
),设旋转角为![]() , 旋转过程中
, 旋转过程中![]() 与
与![]() 交于点
交于点![]() .
.
①当![]() 时,请求出线段
时,请求出线段![]() 的长;
的长;
②当![]() 时,求出线段
时,求出线段![]() 的长;判断此时与
的长;判断此时与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
③当![]() 时,
时,![]() 与
与![]() 相切.
相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形![]() 的两条对角线相交于点
的两条对角线相交于点![]() 轴,垂足为点
轴,垂足为点![]() 正比例函数
正比例函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像相交于
的图像相交于![]() 两点.
两点.

(1)求正比例函数和反比例函数的解析式;
(2)求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b(k≠0)的图象经过A(3,18)和B(﹣2,8)两点.
(1)求一次函数的解析式;
(2)若一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象只有一个交点,求交点坐标.
(m≠0)的图象只有一个交点,求交点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com