
【题目】已知,平面直角坐标系内,点A(a,0),B(b,2),C(0,2),且a、b是方程组![]() 的解,求:
的解,求:
(1)a、b的值.
(2)过点E(6,0)作PE∥y轴,点Q(6,m)是直线PE上一动点,连QA、QB,试用含有m的式子表示△ABQ的面积.
(3)在(2)的条件下.当△ABQ的面积是梯形OABC面积一半时,求Q点坐标.
【答案】(1)a=5,b=3;(2) △ABQ的面积为|m+1|;(3) Q(6,3)或(6,﹣5).
【解析】
(1)解方程组可直接求出a、b的值;
(2)先求出直线AB的解析式为y=﹣x+5,当点Q在AB上时,m=﹣1,然后分当m>﹣1时和m<﹣1时两种情况求解;
(3)计算S梯形OABC,根据△ABQ的面积是梯形OABC面积一半列出方程求m的值即可.
(1)由方程组![]() 两式相加,得a+b=8,
两式相加,得a+b=8,
再与方程组中两式分别相减,得![]() ;
;
(2)由(1)可知,A(5,0),B(3,2),
∴直线AB的解析式为y=﹣x+5,当点Q在AB上时,m=﹣1,
如图1,当m>﹣1时,
过B点作BD⊥x轴,垂足为D,
则S△ABQ=S梯形BDEQ﹣S△ABD﹣S△AQE
=![]() (2+m)×(6﹣3)﹣
(2+m)×(6﹣3)﹣![]() ×2×(5﹣3)﹣
×2×(5﹣3)﹣![]() ×(6﹣5)×m
×(6﹣5)×m
=m+1;
当m<﹣1时,如图2所示,
过点B作BM⊥EQ于点M,
则S△ABQ=S△BMQ﹣S△AEQ﹣S梯形AEMB
=![]() ×(2﹣m)×(6﹣3)﹣
×(2﹣m)×(6﹣3)﹣![]() ×(6﹣5)×(﹣m)﹣
×(6﹣5)×(﹣m)﹣![]() ×(6﹣3+6﹣5)×2
×(6﹣3+6﹣5)×2
=3﹣![]() m+
m+![]() m﹣4
m﹣4
=﹣m﹣1.
综上所述,△ABQ的面积为|m+1|;
(3)∵S梯形OABC=![]() ×(3+5)×2=8,
×(3+5)×2=8,
依题意,得|m+1|=![]() ×8,
×8,
解得m=3或m=﹣5;
∴Q(6,3)或(6,﹣5).


科目:初中数学 来源: 题型:
【题目】某商场对一种新售的手机进行市场问卷调查,其中一个项目是让每个人按A(不喜欢)、B(一般)、C(不比较喜欢)、D(非常喜欢)四个等级对该手机进行评价,图①和图②是该商场采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题:
(1)本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.
(2)图①中,a等于多少?D等级所占的圆心角为多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(徐州中考)如图,在△ABC中,∠ABC=90°,∠BAC=60°,△ACD是等边三角形,E是AC的中点,连接BE并延长交DC于点F,求证:
(1)△ABE≌△CFE;
(2)四边形ABFD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=10,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,AG=2.5,则△CEF的周长为

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3)、B(﹣1,0),请解答下列问题: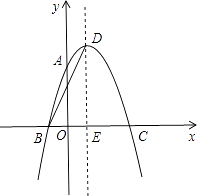
(1)求抛物线的解析式;
(2)抛物线的顶点为D,与x轴的另一交点为C,对称轴交x轴于点E,连接BD,求cos∠DBE;
(3)在直线BD上是否存在点F,使由B、C、F三点构成的三角形与△BDE相似?若存在,求出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c、d均为有理数,其中a是绝对值最小的有理数,b是最小的正整数,c2、4,c、d互为倒数,求:
(1)a×b的值;
(2)a+b+c﹣d的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)
(1)转动钢管得到三角形钢架,如图1,则点A,E之间的距离是米.
(2)转动钢管得到如图2所示的六边形钢架,有∠A=∠B=∠C=∠D=120°,现用三根钢条连接顶点使该钢架不能活动,则所用三根钢条总长度的最小值是米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.

完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.
(1)在图1中请你通过观察、测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后证明你的猜想;
(2)当三角尺沿AC方向平移到图2所示的位置时,一条直角边仍与AC边在同一直线上,另一条直角边交BC边于点D,过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后证明你的猜想;
(3)当三角尺在(2)的基础上沿AC方向继续平移到图3所示的位置(点F在线段AC上,且点F与点C不重合)时,若AG:AB=5:13,BC=4![]() ,求DE+DF的值.
,求DE+DF的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com