
【题目】已知a、b、c、d均为有理数,其中a是绝对值最小的有理数,b是最小的正整数,c2、4,c、d互为倒数,求:
(1)a×b的值;
(2)a+b+c﹣d的值.
科目:初中数学 来源: 题型:
【题目】如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是( )
A.1,2,3
B.1,1, ![]()
C.1,1, ![]()
D.1,2, ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
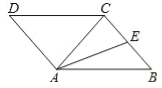
【题目】如图,在ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线.
(1)用无刻度的直尺画出△ABC的高CH(保留画图痕迹);
(2)求△ACE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E. 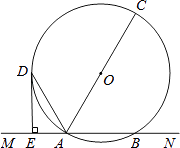
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,平面直角坐标系内,点A(a,0),B(b,2),C(0,2),且a、b是方程组![]() 的解,求:
的解,求:
(1)a、b的值.
(2)过点E(6,0)作PE∥y轴,点Q(6,m)是直线PE上一动点,连QA、QB,试用含有m的式子表示△ABQ的面积.
(3)在(2)的条件下.当△ABQ的面积是梯形OABC面积一半时,求Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在数轴上,从点A出发,沿数轴向右移动3个单位长度到达点C,点B所表示的有理数是5的相反数,按要求完成下列各小题.
(1)请在数轴上标出点B和点C;
(2)求点B所表示的有理数与点C所表示的有理数的乘积;
(3)若将该数轴进行折叠,使得点A和点B重合,则点C和数 所表示的点重合.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1表示同一时刻的韩国首尔时间和北京时间,两地时差为整数.
(1)设北京时间为x(时),首尔时间为y(时),就0≤x≤12,求y关于x的函数表达式,并填写下表(同一时刻的两地时间).
北京时间 | 7:30 | 11:15 | 2:50 |
首尔时间 | 8:30 | 12:15 | 3:50 |
(2)如图2表示同一时刻的英国伦敦时间(夏时制)和北京时间,两地时差为整数.如果现在伦敦(夏时制)时间为7:30,那么此时韩国首尔时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1 , 另两张直角三角形纸片的面积都为S2 , 中间一张正方形纸片的面积为S3 , 则这个平行四边形的面积一定可以表示为( )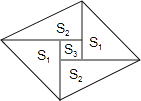
A.4S1
B.4S2
C.4S2+S3
D.3S1+4S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(5,0),菱形OABC的顶点B,C都在第一象限,tan∠AOC= ![]() ,将菱形绕点A按顺时针方向旋转角α(0°<∠α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG.
,将菱形绕点A按顺时针方向旋转角α(0°<∠α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG. 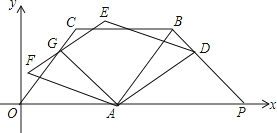
(1)求点B的坐标.
(2)当OG=4时,求AG的长.
(3)求证:GA平分∠OGE.
(4)连结BD并延长交x轴于点P,当点P的坐标为(12,0)时,求点G的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com