
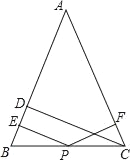
【题目】如图,在△ABC中,AB=AC,CD垂直AB于D,P为BC上的任意一点,过P点分别作PE⊥AB,PF⊥CA,垂足分别为E,F.
(1)若P为BC边中点,则PE,PF,CD三条线段有何数量关系(写出推理过程)?
(2)若P为线段BC上任意一点,则(1)中关系还成立吗?
(3)若P为直线BC上任意一点,则PE,PF,CD三条线段间有何数量关系(请直接写出).
【答案】(1)CD=PE+PF,理由详见解析;(2)成立,理由详见解析;(3)PE﹣PF=CD或PF﹣PE=CD.
【解析】
(1)如图1,连接PA,根据三角形的面积公式列方程即可得到结论;
(2)连接PA,根据三角形的面积公式即可得到结论;
(3)如图2和图3,连接PA,根据三角形的面积列方程即可得到结论.
(1)CD=PE+PF.理由如下:
如图1,连接PA.
∵CD⊥AB于D,PE⊥AB于E,PF⊥AC于F.
∵S△ABC![]() AB×CD,S△PAB
AB×CD,S△PAB![]() AB×PE,S△PAC
AB×PE,S△PAC![]() AC×PF.
AC×PF.
又∵S△ABC=S△PAB+S△PAC,∴![]() AB×CD
AB×CD![]() AB×PE
AB×PE![]() AC×PF.
AC×PF.
∵AB=AC,∴CD=PE+PF.
(2)成立,理由如下:
连接PA.
∵CD⊥AB于D,PE⊥AB于E,PF⊥AC于F.
∵S△ABC![]() AB×CD,S△PAB
AB×CD,S△PAB![]() AB×PE,S△PAC
AB×PE,S△PAC![]() AC×PF.
AC×PF.
又∵S△ABC=S△PAB+S△PAC,∴![]() AB×CD
AB×CD![]() AB×PE
AB×PE![]() AC×PF.
AC×PF.
∵AB=AC,∴CD=PE+PF.
(3)结论:PE﹣PF=CD或PF﹣PE=CD.理由如下:
如图2,连接PA.
∵CD⊥AB于D,PE⊥AB于E,PF⊥AC于F.
∵S△ABC![]() AB×CD,S△PAB
AB×CD,S△PAB![]() AB×PE,S△PAC
AB×PE,S△PAC![]() AC×PF.
AC×PF.
又∵S△ABC=S△PAC﹣S△PAB,∴![]() AB×CD
AB×CD![]() AC×PF
AC×PF![]() AB×PE.
AB×PE.
∵AB=AC,∴CD=PF﹣PE.
如图3,连接PA.
∵CD⊥AB于D,PE⊥AB于E,PF⊥AC于F.
∵S△ABC![]() AB×CD,S△PAB
AB×CD,S△PAB![]() AB×PE,S△PAC
AB×PE,S△PAC![]() AC×PF.
AC×PF.
又∵S△ABC=S△PAB﹣S△PAC,∴![]() AB×CD
AB×CD![]() AB×PE
AB×PE![]() AC×PF.
AC×PF.
∵AB=AC,∴CD=PE﹣PF.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC,△ADE均为等腰直角三角形,点D,E,C在同一直线上,连接BD.
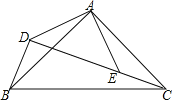
(1)求证:△ADB≌△AEC;
(2)若AD=AE=![]() ,CE=2,求BC的长.
,CE=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了准备“迎新活动”,用700元购买了甲、乙两种小礼品260个,其中购买甲种礼品比乙种礼品少用了100元.
(1)购买乙种礼品花了______元;
(2)如果甲种礼品的单价比乙种礼品的单价高20%,求乙种礼品的单价.(列分式方程解应用题)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:等腰△ABC的底边BC长为6,面积是18,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
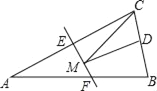
A. 6 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16.
(1)求C点坐标;
(2)如图2,设D为线段OB上一动点,当AD⊥AC时,∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点P,求∠APD的度数.
(3)如图3,当D点在线段OB上运动时,作DM⊥AD交BC于M点,∠BMD、∠DAO的平分线交于N点,则D点在运动过程中,∠N的大小是否变化?若不变,求出其值,若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
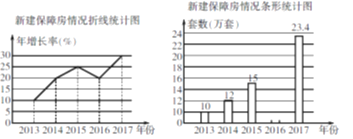
【题目】保障房建设是民心工程,某市从2013年加快保障房建设工程. 现统计该市从2013年到2017年这5年新建保障房情况,绘制成如图所示的折线统计图和不完整的条形统计图.
(1)小颖看了统计图后说:“该市2016年新建保障房的套数比2015年少了.” 你认为小颖的说法正确吗?请说明理由;
(2)求2016年新建保障房的套数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知一个多边形的内角和是它的外角和的 3 倍,求这个多边形的边数.
(2)如图,点F 是△ABC 的边 BC 延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,DE∥AB.请根据已知条件进行推理,分别得出结论,并在括号内注明理由.

(1)∵DE∥AB,( 已知 )
∴∠2= . ( , )
(2)∵DE∥AB,(已知 )
∴∠3= .( , )
(3)∵DE∥AB(已知 ),
∴∠1+ =180°.( , )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com