
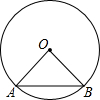
 如图,⊙O的半径OA,OB,且OA⊥OB,连结AB.在⊙O上找一点C,使OA2+AB2=BC2,则∠OAC的度数为
如图,⊙O的半径OA,OB,且OA⊥OB,连结AB.在⊙O上找一点C,使OA2+AB2=BC2,则∠OAC的度数为 解:如图,设圆的半径是r,则AO=r,BO=r,作直径BD,作BC⊙O的弦BC,使∠DBC=30°,作BC关于直径BD的对称线段BE,
解:如图,设圆的半径是r,则AO=r,BO=r,作直径BD,作BC⊙O的弦BC,使∠DBC=30°,作BC关于直径BD的对称线段BE, |
| DE |
 |
| CD |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线y=3x+3与x轴交于点A,与y轴交于点B.过B点作直线BP与x轴正半轴交于点P,取线段OA、OB、OP,当其中一条线段的长是其他两条线段长度的比例中项时,则P点的坐标为
如图,直线y=3x+3与x轴交于点A,与y轴交于点B.过B点作直线BP与x轴正半轴交于点P,取线段OA、OB、OP,当其中一条线段的长是其他两条线段长度的比例中项时,则P点的坐标为查看答案和解析>>
科目:初中数学 来源: 题型:
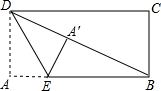 如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为( )
如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为( )A、
| ||
| B、3 | ||
| C、5 | ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
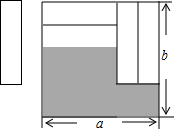 如图,把四张形状大小完全相同的小长方形卡片不重叠地放在一个底面为长方形(长为a,宽为b)的盒子底部,盒子底面未被卡片覆盖的部分用阴影表示,则这两块阴影部分小长方形周长的和为( )
如图,把四张形状大小完全相同的小长方形卡片不重叠地放在一个底面为长方形(长为a,宽为b)的盒子底部,盒子底面未被卡片覆盖的部分用阴影表示,则这两块阴影部分小长方形周长的和为( )| A、a+2b | B、4a |
| C、4b | D、2a+b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com