
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕxOyжаЃЌОиаЮABCDЕФDCБпдкxжсЩЯЃЌDЕузјБъЮЊЃЈЉ6ЃЌ0ЃЉБпABЁЂADЕФГЄЗжБ№ЮЊ3ЁЂ8ЃЌEЪЧBCЕФжаЕуЃЌЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓОЙ§ЕуEЃЌгыADБпНЛгкЕуFЃЎ
ЕФЭМЯѓОЙ§ЕуEЃЌгыADБпНЛгкЕуFЃЎ
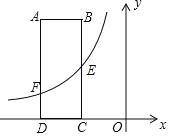
ЃЈ1ЃЉЧѓkЕФжЕМАОЙ§AЁЂEСНЕуЕФвЛДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШєxжсЩЯгавЛЕуPЃЌЪЙPE+PFЕФжЕзюаЁЃЌЪдЧѓГіЕуPЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНгEFЁЂPEЁЂPFЃЌдкжБЯпAEЩЯеввЛЕуQЃЌЪЙЕУSЁїQEFЃНSЁїPEFжБНгаДГіЗћКЯЬѕМўЕФQЕузјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉkЃНЃ12ЃЌyЃНЉ![]() xЃЛЃЈ2ЃЉPЃЈЉ5ЃЌ0ЃЉЃЛЃЈ3ЃЉQЃЈЉ
xЃЛЃЈ2ЃЉPЃЈЉ5ЃЌ0ЃЉЃЛЃЈ3ЃЉQЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈЉ
ЃЉЛђЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШШЗЖЈЕуBЃЌCзјБъЃЌНјЖјЕУГіЕуEзјБъЃЌзюКѓгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіжБЯпAEНтЮіЪНЃЛ
ЃЈ2ЃЉЯШевГіЕуFЙигкxжсЕФЖдГЦЕуFЁфЕФзјБъЃЌНјЖјЧѓГіжБЯпEFЁфЕФНтЮіЪНЃЌНјвЛВНМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЯШЧѓГіЁїPEFЕФУцЛ§ЃЌдйЧѓГіжБЯпEFЕФНтЮіЪНЃЌЩшГіЕуQЕФзјБъЃЌРћгУзјБъЯЕжаЧѓШ§НЧаЮУцЛ§ЕФЗНЗЈНЈСЂЗНГЬЧѓНтЃЌНјЖјЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉдкОиаЮABCDжаЃЌABЃН3ЃЌADЃН8ЃЌ
ЁрCDЃНABЃН3ЃЌBCЃНADЃН8ЃЌ
ЁпDЃЈЉ6ЃЌ0ЃЉЃЌ
ЁрAЃЈЉ6ЃЌ8ЃЉЃЌCЃЈЉ3ЃЌ0ЃЉЃЌBЃЈЉ3ЃЌ8ЃЉЃЌ
ЁпEЪЧBCЕФжаЕуЃЌ
ЁрEЃЈЉ3ЃЌ4ЃЉЃЌ
ЁпЕуEдкЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓЩЯЃЌ
ЕФЭМЯѓЩЯЃЌ
ЁрkЃНЉ3ЁС4ЃНЉ12ЃЌ
ЩшОЙ§AЁЂEСНЕуЕФвЛДЮКЏЪ§ЕФБэДяЪНЮЊyЃНkЁфx+bЃЌ
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ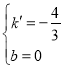 ЃЌ
ЃЌ
ЁрОЙ§AЁЂEСНЕуЕФвЛДЮКЏЪ§ЕФБэДяЪНЮЊyЃНЉ![]() xЃЛ
xЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌгЩЃЈ1ЃЉжЊЃЌkЃНЉ12ЃЌ
ЁрЗДБШР§КЏЪ§ЕФНтЮіЪНЮЊyЃНЉ![]() ЃЌ
ЃЌ
ЁпЕуFЕФКсзјБъЮЊЉ6ЃЌЁрЕуFЕФзнзјБъЮЊ2ЃЌЁрFЃЈЉ6ЃЌ2ЃЉЃЌ
зїЕуFЙигкxжсЕФЖдГЦЕуFЁфЃЌдђFЁфЃЈЉ6ЃЌЉ2ЃЉЃЌ
СЌНгEFЁфНЛxжсгкЕуPЃЌДЫЪБЃЌPE+PFЕФжЕзюаЁЃЌ
ЁпEЃЈЉ3ЃЌ4ЃЉЃЌ
ЁржБЯпEFЁфЕФНтЮіЪНЮЊyЃН2x+10ЃЌ
СюyЃН0ЃЌдђ2x+10ЃН0ЃЌНтЕУxЃНЉ5ЃЌ
ЁрPЃЈЉ5ЃЌ0ЃЉЃЛ

ЃЈ3ЃЉШчЭМ2ЃЌгЩЃЈ2ЃЉжЊЃЌFЁфЃЈЉ6ЃЌЉ2ЃЉЃЌ
ЁпEЃЈЉ3ЃЌ4ЃЉЃЌFЃЈЉ6ЃЌ2ЃЉЃЌ
ЁрSЁїPEFЃНSЁїEFFЁфЉSЁїPFFЁфЃН![]() ЁСЃЈ2+2ЃЉЁСЃЈЉ3+6ЃЉЉ
ЁСЃЈ2+2ЃЉЁСЃЈЉ3+6ЃЉЉ![]() ЃЈ2+2ЃЉЁСЃЈЉ5+6ЃЉЃН4ЃЌ
ЃЈ2+2ЃЉЁСЃЈЉ5+6ЃЉЃН4ЃЌ
ЁпEЃЈЉ3ЃЌ4ЃЉЃЌFЃЈЉ6ЃЌ2ЃЉЃЌ
ЁржБЯпEFЕФНтЮіЪНЮЊyЃН![]() x+6ЃЌ
x+6ЃЌ
гЩЃЈ1ЃЉжЊЃЌОЙ§AЁЂEСНЕуЕФвЛДЮКЏЪ§ЕФБэДяЪНЮЊyЃНЉ![]() xЃЌ
xЃЌ
ЩшЕуQЃЈmЃЌЉ![]() mЃЉЃЌ
mЃЉЃЌ
Й§ЕуQзїyжсЕФЦНааЯпНЛEFгкGЃЌ
ЁрGЃЈmЃЌ![]() m+6ЃЉЃЌ
m+6ЃЉЃЌ
ЁрQGЃН|Љ![]() mЉ
mЉ![]() mЉ6|ЃН|2m+6|ЃЌ
mЉ6|ЃН|2m+6|ЃЌ
ЁпSЁїQEFЃНSЁїPEFЃЌ
ЁрSЁїQEFЃН![]() |2m+6|ЁСЃЈЉ3+6ЃЉЃН4ЃЌ
|2m+6|ЁСЃЈЉ3+6ЃЉЃН4ЃЌ
ЁрmЃНЉ![]() ЛђmЃНЉ
ЛђmЃНЉ![]() ЃЌ
ЃЌ
ЁрQЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈЉ
ЃЉЛђЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЌЪаШЅФъЕквЛМОЖШЦНОљУПдТгЏРћ2ЭђдЊЃЌЕкЖўМОЖШЦНОљУПдТПїЫ№1.5ЭђдЊЃЌЕкШ§МОЖШЦНОљУПдТПїЫ№1.7ЭђдЊЃЌЕкЫФМОЖШЦНОљУПдТгЏРћ2.5ЭђдЊ.
ЃЈ1ЃЉНЋгЏРћМЧЮЊЁА+ЁБЃЌПїЫ№МЧЮЊЁА-ЁБЃЌВЙГфЯТБэЃКЃЈЕЅЮЛЃКЭђдЊЃЉ

ЃЈ2ЃЉетМвГЌЪаШЅФъзмгЏПїЧщПіШчКЮЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
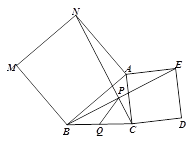
ЁОЬтФПЁПЬНОПЃКШчЭМЃЌЗжБ№вдЁїABCЕФСНБпABКЭACЮЊБпЯђЭтзїе§ЗНаЮABMNКЭе§ЗНаЮACDEЃЌCNЁЂBEНЛгкЕуP. ЧѓжЄЃКЁЯANC = ЁЯABE.
гІгУЃКQЪЧЯпЖЮBCЕФжаЕуЃЌСЌНсPQ. ШєBC = 6ЃЌдђPQ = ___________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПРЯЪІдкКкАхЩЯЪщаДСЫвЛИіе§ШЗЕФбнЫуЙ§ГЬЃЌЫцКѓгУЪжеЦЮцзЁСЫвЛИіЖрЯюЪНЃЌаЮЪНШчЯТЃК
![]()
(1)ЧѓЫљЮцЕФЖрЯюЪНЃЛ
(2)ШєxЮЊе§ећЪ§ЃЌШЮШЁxЕФМИИіжЕВЂЧѓГіЫљЮцЖрЯюЪНЕФжЕЃЌФуФмЗЂЯжЪВУДЙцТЩЃП
(3)ШєЫљЮцЖрЯюЪНЕФжЕЮЊ144ЃЌЧыжБНгаДГіе§ећЪ§xЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЗўзАЕъЙКНјвЛХњМзЁЂввСНжжПюаЭЪБЩаTаєЩРЃЌМзжжПюаЭЙВгУСЫ7800дЊЃЌввжжПюаЭЙВгУСЫ6400дЊЃЌМзжжПюаЭЕФМўЪ§ЪЧввжжПюаЭМўЪ§ЕФ1.5БЖЃЌМзжжПюаЭУПМўЕФНјМлБШввжжПюаЭУПМўЕФНјМлЩй30дЊЃЎ
ЃЈ1ЃЉМзЁЂввСНжжПюаЭЕФTаєЩРИїЙКНјЖрЩйМўЃП
ЃЈ2ЃЉЩЬЕъНјМлЬсИп60%БъМлЯњЪлЃЌЯњЪлвЛЖЮЪБМфКѓЃЌМзПюаЭШЋВПЪлЭъЃЌввПюаЭЪЃгрвЛАыЃЌЩЬЕъОіЖЈЖдввПюаЭАДБъМлЕФЮхелНЕМлЯњЪлЃЌКмПьШЋВПЪлЭъЃЌЧѓЪлЭъ етХњTаєЩРЩЬЕъЙВЛёРћЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕЅЮЛГЄЖШЮЊ1ЕФЗНИёжагаШ§НЧаЮABC.
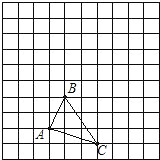
ЃЈ1ЃЉЧыЛГіШ§НЧаЮABCЯђЩЯЦНвЦ3ИёдйЯђгвЦНвЦ2ИёКѓЫљЕУЕНЕФШ§НЧаЮAЁфBЁфCЁфЃЛ
ЃЈ2ЃЉЧывдЕуAЮЊзјБъдЕуНЈСЂЦНУцжБНЧзјБъЯЕЃЈдкЭМжаЛГіЃЉЃЌШЛКѓаДГіЕуBЃЌBЁфЕФзјБъЃЛ
ЃЈ3ЃЉЧѓГіШ§НЧаЮABCЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
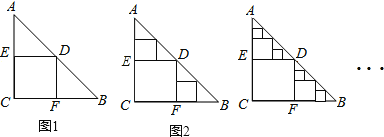
ЁОЬтФПЁПЁїABCЪЧвЛеХЕШбќжБНЧШ§НЧаЮжНАхЃЌЁЯC=RtЁЯЃЌAC=BC=2ЃЌдкетеХжНАхжаМєГівЛИіОЁПЩФмДѓЕФе§ЗНаЮГЦЮЊЕк1ДЮМєШЁЃЌМЧЫљЕУе§ЗНаЮУцЛ§ЮЊs1ЃЈШчЭМ1ЃЉЃЛдкгрЯТЕФRtЁїADEКЭRtЁїBDFжаЃЌЗжБ№МєШЁе§ЗНаЮЃЌЕУЕНСНИіЯрЭЌЕФе§ЗНаЮЃЌГЦЮЊЕк2ДЮМєШЁЃЌВЂМЧетСНИіе§ЗНаЮУцЛ§КЭЮЊs2ЃЈШчЭМ2ЃЉЃЛМЬајВйзїЯТШЅЁЃЛдђЕк10ДЮМєШЁЪБЃЌs10= ЃЛЕк2012ДЮМєШЁКѓЃЌгрЯТЕФЫљгааЁШ§НЧаЮЕФУцЛ§жЎКЭЪЧ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
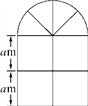
ЁОЬтФПЁПЃЈ12ЗжЃЉШчЭМЪЧФГжжДАЛЇЕФаЮзДЃЌЦфЩЯВПЪЧАыдВаЮЃЌЯТВПЪЧБпГЄЯрЭЌЕФЫФИіаЁе§ЗНаЮЃЌвбжЊЯТВПЕФаЁе§ЗНаЮЕФБпГЄЮЊamЃЌМЦЫуЃК
ЃЈ1ЃЉДАЛЇЕФУцЛ§ЃЛ
ЃЈ2ЃЉДАПђЕФзмГЄЃЛ
ЃЈ3ЃЉШєaЃН1ЃЌДАЛЇЩЯАВзАЕФЪЧВЃСЇЃЌВЃСЇУПЦНЗНУз25дЊЃЌДАПђУПУз20дЊЃЌДАПђЕФКёЖШВЛМЦЃЌЧѓжЦзїетжжДАЛЇашвЊЕФЗбгУЪЧЖрЩйдЊЃЈІаШЁ3.14ЃЌНсЙћБЃСєећЪ§ЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
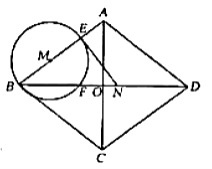
ЁОЬтФПЁПШчЭМЃЌСтаЮ![]() жаЃЌЖдНЧЯп
жаЃЌЖдНЧЯп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЌЖЏЕу
ЃЌЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌбиЯпЖЮ
ГіЗЂЃЌбиЯпЖЮ![]() вд
вд![]() ЕФЫйЖШЯђЕу
ЕФЫйЖШЯђЕу![]() дЫЖЏЃЌЭЌЪБЖЏЕу
дЫЖЏЃЌЭЌЪБЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌбиЯпЖЮ
ГіЗЂЃЌбиЯпЖЮ![]() вд
вд![]() ЕФЫйЖШЯђЕу
ЕФЫйЖШЯђЕу![]() дЫЖЏЃЌЕБЦфжавЛИіЖЏЕуЭЃжЙдЫЖЏЪБСэвЛИіЖЏЕувВЫцжЎЭЃжЙ.ЩшдЫЖЏЪБМфЮЊ
дЫЖЏЃЌЕБЦфжавЛИіЖЏЕуЭЃжЙдЫЖЏЪБСэвЛИіЖЏЕувВЫцжЎЭЃжЙ.ЩшдЫЖЏЪБМфЮЊ![]() ЃЌвдЕу
ЃЌвдЕу![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ЮЊАыОЖЕФЁб
ЮЊАыОЖЕФЁб![]() гыЩфЯп
гыЩфЯп![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ЗжБ№НЛгкЕу
ЗжБ№НЛгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() .
.
ЃЈ1ЃЉЧѓ![]() ЕФГЄЃЈгУКЌга
ЕФГЄЃЈгУКЌга![]() ЕФДњЪ§ЪНБэЪОЃЉЃЌВЂЧѓГі
ЕФДњЪ§ЪНБэЪОЃЉЃЌВЂЧѓГі![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЕБ![]() ЮЊКЮжЕЪБЃЌЯпЖЮ
ЮЊКЮжЕЪБЃЌЯпЖЮ![]() гыЁб
гыЁб![]() ЯрЧаЃП
ЯрЧаЃП
ЃЈ3ЃЉШєЁб![]() гыЯпЖЮ
гыЯпЖЮ![]() жЛгавЛИіЙЋЙВЕуЃЌЧѓ
жЛгавЛИіЙЋЙВЕуЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com