
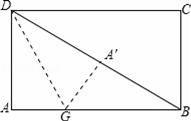
如图,矩形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边与对角线BD重合,折痕为DG,则AG的长为 .

科目:初中数学 来源: 题型:
为了迎接“五•一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如表:
| 运动鞋价格 | 甲 | 乙 |
| 进价(元/双) | m | m﹣20 |
| 售价(元/双) | 240 | 160 |
已知:用3600元购进甲种运动鞋的数量与用3000元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21600元,且不超过22440元,问该专卖店有多少种进货方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com