
如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为3,则阴影部分的面积为 (结果保留π).
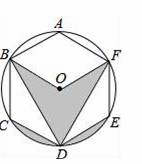
3π【考点】正多边形和圆;扇形面积的计算.
【分析】首先连接OC,OE,分别交BD,DF于点M,N,易证得S△OBM=S△DCM,同理:S△OFN=S△DEN,则可得S阴影=S扇形OCE.
【解答】解:连接OC,OE,分别交BD,DF于点M,N,
∵正六边形ABCDEF内接于⊙O,
∴∠BOC=60°,∠BCD=∠COE=120°,
∵OB=OC,
∴△OBC是等边三角形,
∴∠OBC=∠OCB=60°,
∴∠OCD=∠OCB,
∵BC=CD,
∴∠CBD=∠CDM=30°,BM=DM,
∴∠OBM=30°,S△DCM=S△BCM,
∴∠OBM=∠CBD,
∴OM=CM,
∴S△OBM=S△BCM,
∴S△OBM=S△DCM,
同理:S△OFN=S△DEN,
∴S阴影=S扇形OCE=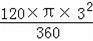
 =3π.
=3π.
故答案为:3π.
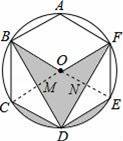

【点评】此题考查了正多边形与圆的知识以及扇形的面积公式.注意证得S阴影=S扇形OCE是关键.


科目:初中数学 来源: 题型:
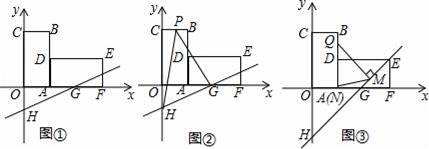
如图①,平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴的正半轴上,点B的坐标为(2,4),将矩形OABC绕着点A顺时针旋转90°得到矩形AFED,直线y=kx+b经过点G(4,0),交y轴于点H.
(1)点D、E的坐标分别为 .
(2)当直线GH经过EF中点K时,如图②,动点P从点C出发,沿着折线C﹣B﹣D以每秒1个单位速度向终点D运动,连结PH、PG,设点P运动的时间为t(秒),△PGH的面积为S(平方单位).
①求直线GH所对应的函数关系式.
②求S与t之间的函数关系式.
(3)当直线GH经过点E时,如图③,点Q是射线B﹣D﹣E﹣F上的点,过点Q作QM⊥GH于点M,作QN⊥x轴于点N,当△QMN为等腰三角形时,直接写出点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.
(1)如果随机翻1张牌,那么抽中20元奖品的概率为 25%
(2)如果随机翻2张牌,且第一次翻过的牌不再参加下次翻牌,则所获奖品总值不低于30元的概率为多少?


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com