
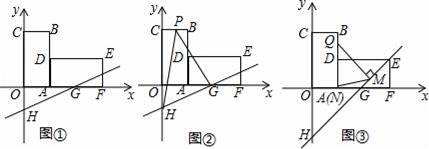
��ͼ�٣�ƽ��ֱ������ϵ�У�����OABC�ı�OA��OC�ֱ���x�ᡢy����������ϣ���B������Ϊ��2��4����������OABC���ŵ�A˳ʱ����ת90��õ�����AFED��ֱ��y=kx+b������G��4��0������y���ڵ�H��
��1����D��E������ֱ�Ϊ������
��2����ֱ��GH����EF�е�Kʱ����ͼ�ڣ�����P�ӵ�C��������������C��B��D��ÿ��1����λ�ٶ����յ�D�˶�������PH��PG�����P�˶���ʱ��Ϊt���룩����PGH�����ΪS��ƽ����λ����
����ֱ��GH����Ӧ�ĺ�����ϵʽ��
����S��t֮��ĺ�����ϵʽ��
��3����ֱ��GH������Eʱ����ͼ�ۣ���Q������B��D��E��F�ϵĵ㣬����Q��QM��GH�ڵ�M����QN��x���ڵ�N������QMNΪ����������ʱ��ֱ��д����Q�����꣮

�����㡿�ı����ۺ��⣮
����������1���ɾ��ε����ʺ�ѡת�����ʼ��ɣ�
��2�����ô���ϵ�������GH�Ľ���ʽ�������ε�������������������ε�����ĺͻ����㣻
��3�������˶��ص��ͼ�ε����ʣ�ȷ������Q��N��M�����꣬���������ľ��빫ʽ�����Ӧ��ȣ���QMNΪ���������Σ��������������������⣬���ɣ�
����𡿣�1���⣺�߾���OABC���ŵ�A˳ʱ����ת90��õ�����AFED����B��2��4����
��OA=AD=2��OC=AF=4��
��D��2��2����E��6��2����
�ʴ�ΪD��2��2����E��6��2����
��2���ٽ⣺��E��6��2����G��4��0����
��K��6��1����
��ֱ��y=kx+b������G��K��
��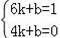
 ��
��
��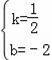
 ��
��
��ֱ��GH�Ľ���ʽΪy=
 x��2��
x��2��
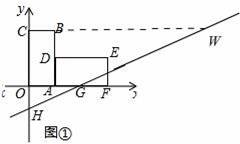

�ڵ�0��t��2ʱ���ӳ�CB��HG��W����ͼ1��
S��PHG=S��SHW��S��HCP��S��PGW=
 [[6��12��6t��4��12��t��]=��t+12��
[[6��12��6t��4��12��t��]=��t+12��
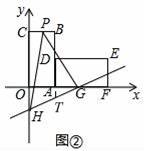

�ڵ�2��t��4ʱ���ӳ�BA��HG��T����ͼ2��
S��PHG=S��PTH+S��PGT=
 ��4��7��t��=��2t+14��
��4��7��t��=��2t+14��
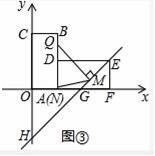

��3���⣻�ٵ�0��t��2ʱ����ͼ3��
�����⣬��N��2��0����Q��2��4��t����M��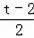
 ��
��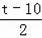
 ����
����
��QN2=��4��t��2��MN2=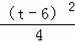
 +
+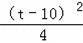
 ��QM2=
��QM2=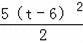
 ��
��
������QN=QMʱ����QN2=QM2��
�ࣨ4��t��2=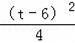
 +
+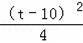
 ��
��
��t=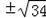
 ���ᣩ��
���ᣩ��
������QN=QMʱ������ͬ����һ������t=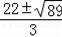
 ���ᣩ��
���ᣩ��
������MN=QMʱ������ͬ����һ�����õ������⣬
�ڵ�2��t��6ʱ��
�����⣬��N��t��0����Q��t��2����M��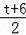
 ��
��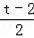
 ����
����
�����͢٣���һ���������������
������QN=QMʱ��t=6+2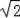
 ���ᣩ����t=6��2
���ᣩ����t=6��2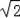
 ��Q��6��2
��Q��6��2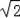
 ��2����
��2����
������QN=MNʱ��t=��8���ᣩ��t=2����Q��2��2����
������QM=MNʱ��t=4����Q��4��2����
�ڵ�6��t��8ʱ��
�����⣬��N��6��0����Q��6��8��t����M��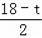
 ����
����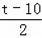
 ����
����
�����͢٣���һ���������������
������QN=QMʱ��t=10+2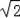
 ���ᣩ����t=10��2
���ᣩ����t=10��2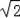
 ��Q��6��2
��Q��6��2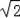
 ��2����
��2����
������QN=MNʱ��t=6���ᣩ��t=10���ᣩ
������QM=MNʱ��t=8���ᣩ��
��Q��6��2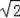
 ��2����Q��2��2����Q��4��2����Q��6��2
��2����Q��2��2����Q��4��2����Q��6��2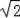
 ��2����
��2����
���������������ı��ε��ۺ��⣬�漰�������ľ��빫ʽ������ϵ������ļ��㷽�����ֶη�������ۣ��Ȿ��Ĺؼ�����t��ʾ���������ͷ����������ļ������Ƚϴ�
��


 ȫ��������ϵ�д�
ȫ��������ϵ�д� һ��һ����ʱ���ϵ�д�
һ��һ����ʱ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ʾ��DE��BC�� EF��AB��ͼ�����BFE�����Ľǹ��� ( )
EF��AB��ͼ�����BFE�����Ľǹ��� ( )
A��3�� B��2�� C��5�� D��4��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
Ϊ��ӭ�ӡ���•һ��С���ٵĹ���߷壮ij�˶�Ʒ��ר�����������ס��������˶�Ь�����мס��������˶�Ь�Ľ��ۺ��ۼ������
| �˶�Ь�۸� | �� | �� |
| ���ۣ�Ԫ/˫�� | m | m��20 |
| �ۼۣ�Ԫ/˫�� | 240 | 160 |
��֪����3600Ԫ���������˶�Ь����������3000Ԫ���������˶�Ь��������ͬ��
��1����m��ֵ��
��2��Ҫʹ�����ļס��������˶�Ь��200˫������������=�ۼ۩����ۣ�������21600Ԫ���Ҳ�����22440Ԫ���ʸ�ר�����ж����ֽ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ƽ���ı��εĶԽ��߳�Ϊx��y��һ�߳�Ϊ12����x��y��ֵ�����ǣ�������
A��8��14 B��10��14 C��18��20 D��10��34
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ij��¥CD�봦���洹ֱ��Ҫ�ڸ�¥ǰ�ĵ���A����װij����ƣ���װ����Ʒ����Ĺ������������нǡ�DACΪ70�㣬������������С�нǡ�DABΪ35�㣬Ҫʹ��Ʒ���ʱ�����ڸ�¥�ϵ������BCΪ50�ף���A������¥�ľ���AD���������ȷ��0.1�ף�
���ο����ݣ�sin70��=0.94��cos70��=0.34��tan70��=2.75��sin35��=0.57��cos35��=0.82��tan35��=0.70��
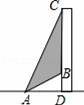

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����������ABCDEF�ڽ��ڡ�O������O�İ뾶Ϊ3������Ӱ���ֵ����Ϊ��������������У���
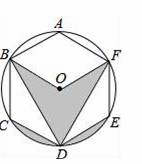
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪�ݺ��� ��ͼ�����
��ͼ�����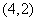 ����
����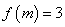 ����ʵ��
����ʵ��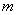 ��ֵΪ�� ��
��ֵΪ�� ��
A��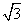 B��
B��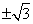 ���� C��
���� C��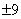 ���� D��
���� D��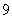
�����������������õ�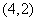 ��ú����Ľ���ʽ��������
��ú����Ľ���ʽ��������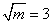 �������
�������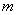 ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com