
【题目】已知数轴上顺次有![]() 、
、![]() 、
、![]() 三点,分别表示数
三点,分别表示数![]() 、
、![]() 、
、![]() ,并且满足
,并且满足![]() ,
,![]() 与
与![]() 互为相反数.一只电子小蜗牛从
互为相反数.一只电子小蜗牛从![]() 点向正方向移动,速度为2个单位/秒.
点向正方向移动,速度为2个单位/秒.
(1)请求出![]() 、
、![]() 、
、![]() 三点分别表示的数.
三点分别表示的数.
(2)运动多少秒时,小蜗牛到点![]() 的距离为1个单位长度.
的距离为1个单位长度.
(3)设点![]() 在数轴上点A的右边,且点
在数轴上点A的右边,且点![]() 分别到点
分别到点![]() 、点
、点![]() 、点
、点![]() 的距离之和是20,那么点
的距离之和是20,那么点![]() 所表示的数是_____.
所表示的数是_____.
【答案】(1) -12,-5,5;(2) 3秒或4秒;(3) -2或-8.
【解析】
(1)根据非负的几个数之和为0,则每个数都为0,再根据![]() 与
与![]() 互为相反数,求出c即可;
互为相反数,求出c即可;
(2)先算出AB的距离,再算出蜗牛走的路程,最后求时间即可;
(3)先由题意得到,![]() ,设P为x,分类讨论x的大小,解绝对值方程即可.
,设P为x,分类讨论x的大小,解绝对值方程即可.
解:(1)由题意得:a+12=0,b+5=0,解得a=-12,b=-5
又∵b与c互为相反数
∴c=5,
∴A,B,C三点分别表示的数是-12,-5,5.
(2)如图:
![]()
可知:AB=7
小蜗牛到点![]() 的距离为1个单位长度时,所走的路程为:6个或者8个单位长度;
的距离为1个单位长度时,所走的路程为:6个或者8个单位长度;
又小蜗牛的爬行速度为2个单位/秒,
所以所用时间为3秒或4秒
(3)∵点![]() 分别到点
分别到点![]() 、点
、点![]() 、点
、点![]() 的距离之和是20,
的距离之和是20,
∴![]()
∵![]() 在数轴上点A的右边
在数轴上点A的右边
∴P表示的数大于-12
设P表示的数为x
①当x≥5时,由![]() ,得x+12+x+5+x-5=20,
,得x+12+x+5+x-5=20,
解得x=![]() (不合题意舍去)
(不合题意舍去)
②当-5<x<5时,由![]() ,得x+12+x+5+5-x=20,
,得x+12+x+5+5-x=20,
解得x=-2,即点P在数轴上所表示的数是-2.
③当-12<x<-5时,由![]() ,得x+12-x-5+5-x=20,解得x=-8,即点P在数轴上所表示的数是-8.
,得x+12-x-5+5-x=20,解得x=-8,即点P在数轴上所表示的数是-8.
综上,P表示的数为-2或-8.


科目:初中数学 来源: 题型:
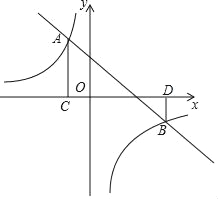
【题目】如图,直线y=﹣x+2与反比例函数y=![]() (k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
(k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
(1)求a,b的值及反比例函数的解析式;
(2)若点P在直线y=﹣x+2上,且S△ACP=S△BDP,请求出此时点P的坐标;
(3)在x轴正半轴上是否存在点M,使得△MAB为等腰三角形?若存在,请直接写出M点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以顶点A为圆心,AD长为半径,在AB边上截取AE=AD,用尺规作图法作出∠BAD的角平分线AG,若AD=5,DE=6,则AG的长是_________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组为了了解本校学生参加课外体育锻炼情况,随机抽取本校40名学生进行问卷调查,统计整理并绘制了如下两幅尚不完整的统计图:

根据以上信息解答下列问题:
(1)课外体育锻炼情况统计图中,“经常参加”所对应的圆心角的度数为 ;“经常参加课外体育锻炼的学生最喜欢的一种项目”中,喜欢足球的人数有 人,补全条形统计图.
(2)该校共有1200名学生,请估计全校学生中经常参加课外体育锻炼并喜欢的项目是乒乓球的人数有多少人?
(3)若在“乒乓球”、“篮球”、“足球”、“羽毛球”项目中任选两个项目成立兴趣小组,请用列表法或画树状图的方法求恰好选中“乒乓球”、“篮球”这两个项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,这是网上盛传的一个关于数学的诡辩问题截图,表1是它的示意表.我们一起来解答“为什么多出了2元".

花去 | 剩余 | |
买牛肉 | 40元 | 60元 |
买猪脚 | 30元 | 30元 |
买蔬菜 | 18元 | 12元 |
买调料 | 12元 | 0元 |
总计 | 100元 | 102元 |
表1
花去 | 剩余 | |
买牛肉 | 40元 | 60元 |
买猪脚 | 30元 | 30元 |
买蔬菜 | 元 | 元 |
买调料 | 元 | 0元 |
总计 | 100元 | 103元 |
表2
花去 | 剩余 | |
买物品1 | a元 | x元 |
买物品2 | b元 | y元 |
买物品3 | c元 | z元 |
买物品4 | d元 | 0元 |
总计 | 100元 | w元 |
表3
花去 | 剩余 | |
买牛肉 | 元 | 元 |
买猪脚 | 元 | 元 |
买蔬菜 | 元 | 元 |
买调料 | 元 | 元 |
总计 | 元 | / |
表4
(1)为了解释“剩余金额总计”与“我手里有100元"无关,请按要求填写表2中的空格.
(2)如表3中,直接写出各代数式的值: .
①a+b+c+d=_ ;
②a+x=__ ;
③a+b+y=_ ;
④a+b+c+z=_ 。
(3)如表3中,a、b、c、d都是正整数,则w的最大值等于_ ,最小值等于_ ,由此可以知道“为什么多出了2元”只是一个诡辩而已.
(4)我们将“花去”记为“一”,“剩余”记为“+”,请在表4中将表1数据重新填写.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有![]() 三点分别表示数
三点分别表示数![]() ,且
,且![]() 满足
满足![]()
![]() .两只电子蚂蚁甲、乙分别从
.两只电子蚂蚁甲、乙分别从![]() 两点同时出发相向而行,若甲的速度为
两点同时出发相向而行,若甲的速度为![]() 个单位/秒,乙的速度为
个单位/秒,乙的速度为![]() 个单位/秒.
个单位/秒.
(1)求![]() 的值并在数轴上标出
的值并在数轴上标出![]() 三点.
三点.

(2)问甲、乙在数轴上的哪个点相遇?
(3)问多少秒后,甲到![]() 的距离为
的距离为![]() 个单位?
个单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店用1050元购进第一批某种钢笔,很快卖完,又用1440元购进第二批该种钢笔,但第二批每支钢笔的进价是第一批进价的1.2倍,数量比第一批多了10支。
(1)求第一批每支钢笔的进价是多少元?
(2)第二批钢笔按24元/支的价格销售,销售一定数量后,根据市场情况,商店决定对剩余的钢笔全按8折一次性打折销售,但要求第二批钢笔的利润率不低于20%,问至少销售多少支后开始打折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简题.
(1)合并下列同类项: 4a2-3b2+2ab-4a2-3b2+5ba
(2)先化简,再求值:2(3x2﹣4xy)﹣4(2x2﹣3xy﹣1),其中|x﹣1|+(y+2)2=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国移动公司开设适合普通用户的两种通讯业务分别是:“全球通”用户先缴![]() 元月租,然后每分钟通话费用
元月租,然后每分钟通话费用![]() 元;“神州行”用户不用缴纳月租费,每分钟通话
元;“神州行”用户不用缴纳月租费,每分钟通话![]() 元.(通话均指拨打本地电话)
元.(通话均指拨打本地电话)
![]() 设一个月内通话时间约为
设一个月内通话时间约为![]() 分钟(
分钟(![]() 且
且![]() 为整数),求这两种用户每月需缴的费用分别是多少元?(用含
为整数),求这两种用户每月需缴的费用分别是多少元?(用含![]() 的式子表示)
的式子表示)
![]() 若张老师一个月通话约
若张老师一个月通话约![]() 分钟,请你给他提个建议,应选择哪种移动通讯方式合算一些?并说明理由.
分钟,请你给他提个建议,应选择哪种移动通讯方式合算一些?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com