
【题目】如图,在数轴上有两点A、B,点B在点A的右侧,且AB=10,点A表示的数为﹣6.动点P从点A出发,以每秒4个单位长度的速度沿数轴向右匀速运动.
(1)写出数轴上点B表示的数;
(2)经过多少时间,线段AP和BP的长度之和为18?
![]()
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,如果对角线AC和BD相交并且相等,那么我们把这样的四边形称为等角线四边形.
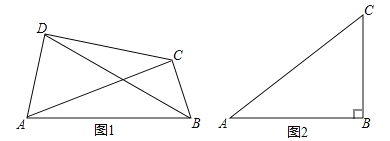
(1)①在“平行四边形、矩形、菱形”中, 一定是等角线四边形(填写图形名称);
②若M、N、P、Q分别是等角线四边形ABCD四边AB、BC、CD.DA的中点,当对角线AC、BD还要满足 时,四边形MNPQ是正方形.
(2)如图2,已知△ABC中,∠ABC=90°,AB=4,BC=3,D为平面内一点.
①若四边形ABCD是等角线四边形,且AD=BD,则四边形ABCD的面积是 ;
②设点E是以C为圆心,1为半径的圆上的动点,若四边形ABED是等角线四边形,写出四边形ABED面积的最大值,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与y轴交于点A(0,﹣4),与x轴相交于B(﹣2,0)、C(4,0)两点,O为坐标原点.
与y轴交于点A(0,﹣4),与x轴相交于B(﹣2,0)、C(4,0)两点,O为坐标原点.
(1)求抛物线的解析式;
(2)设点E在x轴上,∠OEA+∠OAB=∠ACB,求BE的长;
(3)如图2,将抛物线y=ax2+bx+c向右平移n(n>0)个单位得到的新抛物线与x轴交于M、N(M在N左侧),P为x轴下方的新抛物线上任意一点,连PM、PN,过P作PQ⊥MN于Q,![]() 是否为定值?请说明理由.
是否为定值?请说明理由.
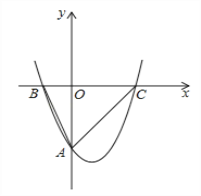
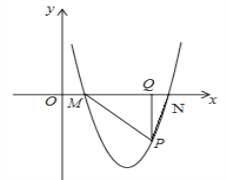
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
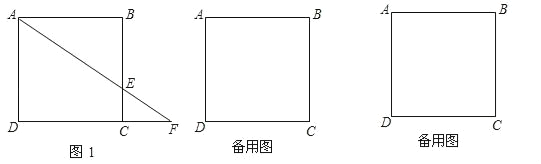
【题目】已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连接AE交射线DC于点F,若△ABE沿直线AE翻折,点B落在点B1处.
(1)如图1,若点E在线段BC上,求CF的长;
(2)求sin∠DAB1的值;
(3)如果题设中“BE=2CE”改为“![]() =x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
=x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一种节能型轿车的油箱加满天然气后,油箱中的剩余天然气量![]() (升)与轿车行驶路程
(升)与轿车行驶路程![]() (千米)之间的关系如图所示,根据图象回答下列问题:
(千米)之间的关系如图所示,根据图象回答下列问题:
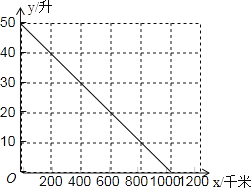
(1)这种轿车的油箱最多能装______升天然气,加满天然气后可供轿车行驶______千米.
(2)轿车每行驶200千米消耗天然气________升.
(3)写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地的一种绿色蔬菜,在市场上若直接销售,每吨利润为1000元,经粗加工后销售,每吨利润4000元,经精加工后销售, 每吨利润为7000元.当地一家公司现有这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨, 如果对蔬菜进行精加工,每天可加工6吨,但每天两种方式不能同时进行.受季节等条件的限制,必须用15天时间将这批蔬菜全部销售或加工完毕.为此,公司研制了三种方案:
方案1:将蔬菜全部进行粗加工;
方案2:尽可能地对蔬菜进行精加工,没来得及加工的蔬菜,在市场上直接出售;
方案3:将一部分蔬菜进行精加工, 其余蔬菜进行粗加工,并刚好15天完成.
如果你是公司经理,你会选择哪一种方案? 请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为4,E为BC边上一点,BE=3,M为线段AE上一点,射线BM交正方形的一边于点F,且BF=AE,则BM的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛是我国固有领土,现在我边海渔民要在钓鱼岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+![]() )海里的C处,为了防止某国海警干扰,请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向,A位于B的北偏西30°方向,求A、C之间的距离.
)海里的C处,为了防止某国海警干扰,请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向,A位于B的北偏西30°方向,求A、C之间的距离.
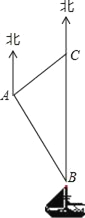
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com