
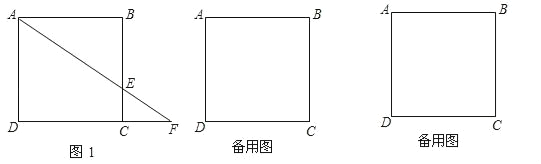
【题目】已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连接AE交射线DC于点F,若△ABE沿直线AE翻折,点B落在点B1处.
(1)如图1,若点E在线段BC上,求CF的长;
(2)求sin∠DAB1的值;
(3)如果题设中“BE=2CE”改为“![]() =x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
=x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
【答案】(1)![]() ;(2) ①
;(2) ①![]() , ②
, ②![]() ;(3)见解析.
;(3)见解析.
【解析】分析:(1)利用平行线性质以及线段比求出CF的值;
(2)本题要分两种方法讨论:①若点E在线段BC上;②若点E在边BC的延长线上.需运用勾股定理求出与之相联的线段;
(3)本题分两种情况讨论:若点E在线段BC上,y=![]() ,自变量取值范围为x>0;若点E在边BC的延长线上,y=
,自变量取值范围为x>0;若点E在边BC的延长线上,y=![]() ,自变量取值范围为x>1.
,自变量取值范围为x>1.
详解:(1)∵AB∥DF,
∴![]() ,
,
∵BE=2CE,AB=3,
∴![]() ,
,
∴CF=![]() ;
;
(2)①若点E在线段BC上,如图1,设直线AB1与DC相交于点M.
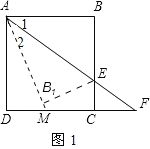
由题意翻折得:∠1=∠2.
∵AB∥DF,
∴∠1=∠F,
∴∠2=∠F,
∴AM=MF.
设DM=x,则CM=3-x.
又∵CF=1.5,
∴AM=MF=![]() -x,
-x,
在Rt△ADM中,AD2+DM2=AM2,
∴32+x2=(![]() -x)2,
-x)2,
∴x=![]() ,
,
∴DM=![]() ,AM=
,AM=![]() ,
,
∴sin∠DAB1=![]() ;
;
②若点E在边BC的延长线上,如图2,设直线AB1与CD延长线相交于点N.
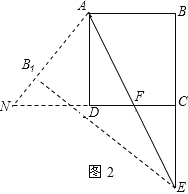
同理可得:AN=NF.
∵BE=2CE,
∴BC=CE=AD.
∵AD∥BE,
∴![]() ,
,
∴DF=FC=![]() ,
,
设DN=x,则AN=NF=x+![]() .
.
在Rt△ADN中,AD2+DN2=AN2,
∴32+x2=(x+![]() )2,
)2,
∴x=![]() .
.
∴DN=![]() ,AN=
,AN=![]() ,sin∠DAB1=
,sin∠DAB1=![]() ;
;
(3)y=![]() ,自变量取值范围为x>0;若点E在边BC的延长线上,y=
,自变量取值范围为x>0;若点E在边BC的延长线上,y=![]() ,自变量取值范围为x>1.
,自变量取值范围为x>1.


科目:初中数学 来源: 题型:
【题目】如图,已知线段![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点,点
上的一个动点,点![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.
(1)若点![]() 恰好是
恰好是![]() 中点,则
中点,则![]()
![]() ;
;
(2)若![]() ,求
,求![]() 的长;
的长;
(3)试利用“字母代替数”的方法,说明不论![]() 取何值(不超过
取何值(不超过![]() ),
),![]() 的长不变.
的长不变.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个汉字“互”字,其中,AB∥CD,∠1=∠2,∠MGH=∠MEF.

求证:∠MEF=∠GHN.
证明:∵ AB∥CD(已知)
∴∠1=∠3( )
又∵∠1=∠2(已知)
∴∠2=∠3( )
∴ME∥HN ( )
∴∠MGH=∠ ( )( )
又∵∠MGH=∠MEF (已知)
∴∠MEF=∠GHN( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y=![]() 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
(1)危险检测表在气体泄漏之初显示的数据是 ;
(2)求反比例函数y=![]() 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某个图形是按下面方法连接而成的:(0,0)→(2,0);(1,0)→(0,﹣1);(1,1)→(1,﹣2);(1,0)→(2,﹣1).
(1)请连接图案,它是一个什么汉字?
(2)作出这个图案关于y轴的轴对称图形,并写出新图案相应各端点的坐标,你得到一个什么汉字?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有两点A、B,点B在点A的右侧,且AB=10,点A表示的数为﹣6.动点P从点A出发,以每秒4个单位长度的速度沿数轴向右匀速运动.
(1)写出数轴上点B表示的数;
(2)经过多少时间,线段AP和BP的长度之和为18?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
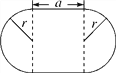
【题目】一个花坛的形状如图所示,它的两端是半径相等的半圆,求:
(1)花坛的周长l;
(2)花坛的面积S;
(3)若a=8m,r=5m,求此时花坛的周长及面积(π取3.14).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.

(1)求∠MON的大小.
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com