[题目]填在上面各正方形中的四个数之间都有相同的规律.根据这种规律.的值应是．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】填在上面各正方形中的四个数之间都有相同的规律，根据这种规律，的值应是__________．

【答案】

【解析】

先根据前3个正方形找出规律，再将18和m代入找出的规律中计算即可得出答案.

第一个图可得，第一行第一个数为0，第二行第一个数为2，第一行第二个数为4，第二行第二个数为2×4-0=8；

第二个图可得，第一行第一个数为2，第二行第一个数为4，第一行第二个数为6，第二行第二个数为4×6-2=22；

第三个图可得，第一行第一个数为4，第二行第一个数为6，第一行第二个数为8，第二行第二个数为6×8-4=44

…

故第n个图中，第一行第一个数为2n-2，第二行第一个数为2n，第一行第二个数为2n+2，第二行第二个数为2n×(2n+2)-(2n-2)；

所求为第10个图，所以第10个图中，第一行第一个数为18，第二行第一个数为20，第一行第二个数为22，第二行第二个数为20×22-18=422；

故答案为422.

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】规律发现：

在数轴上

（1）点M表示的数是2，点N表示的数是8，则线段MN的中点P表示的数为______；

（2）点M表示的数是﹣3，点N表示的数是7，则线段MN的中点P表示的数为_____；发现：点M表示的数是a，点N表示的数是b，则线段MN的中点P表示的数为______．

直接运用：

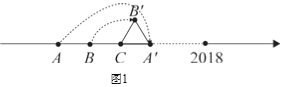
将数轴按如图1所示，从点A开始折出一个等边三角形A'B'C，设点A表示的数为x﹣3，点B表示的数为2x+1，C表示的数为x﹣1，则x值为_____，若将△A'B'C从图中位置向右滚动，则数2018对应的点将与△A'B'C的顶点_______重合．

类比迁移：

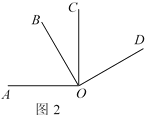
如图2：OA⊥OC，OB⊥OD，∠COD＝60°，若射线OA绕O点以每秒15°的速度顺时针旋转，射线OB绕O点以每秒10°的速度顺时针旋转，射线OC绕O点以每秒5°的速度逆时针旋转，三线同时旋转，当一条射线与射线OD重合时，三条射线同时停止运动．

①求射线OC和射线OB相遇时，∠AOB的度数；

②运动几秒时，射线OA是∠BOC的平分线？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】甲、乙两地相距300千米，一辆货车和一辆轿车分别从甲地开往乙地（轿车的平均速度大于货车的平均速度），如图，线段、折线分别表示两车离甲地的距离（单位：千米）与时间（单位：小时）之间的函数关系.

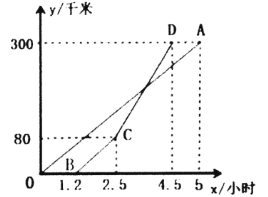
（1）线段与折线中，______（填线段或折线）表示货车离甲地的距离与时间之间的函数关系.

（2）求线段的函数关系式（标出自变量取值范围）；

（3）货车出发多长时间两车相遇？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在等腰直角中，，为的中点，将折叠，使点与点重合，为折痕，则的值是（）

A. B. C. D.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图1，已知抛物线与y轴交于点A（0，﹣4），与x轴相交于B（﹣2，0）、C（4，0）两点，O为坐标原点．

（1）求抛物线的解析式；

（2）设点E在x轴上，∠OEA+∠OAB=∠ACB，求BE的长；

（3）如图2，将抛物线y=ax2+bx+c向右平移n（n＞0）个单位得到的新抛物线与x轴交于M、N（M在N左侧），P为x轴下方的新抛物线上任意一点，连PM、PN，过P作PQ⊥MN于Q，是否为定值？请说明理由．

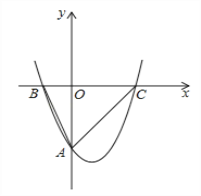
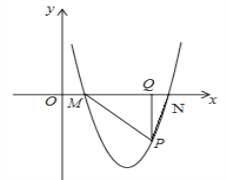
图1 图2

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某校实验课程改革，初三年级设罝了A，B，C，D四门不同的拓展性课程（每位学生只选修其中一门，所有学生都有一门选修课程），学校摸底调査了初三学生的选课意向，并将调查结果绘制成两个不完整的统计图，问该校初三年级共有多少学生？其中要选修B、C课程的各有多少学生？

查看答案和解析>>

科目：初中数学 来源： 题型：

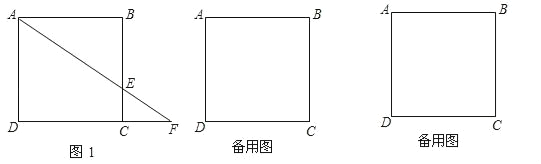
【题目】已知边长为3的正方形ABCD中，点E在射线BC上，且BE=2CE，连接AE交射线DC于点F，若△ABE沿直线AE翻折，点B落在点B1处．

（1）如图1，若点E在线段BC上，求CF的长；

（2）求sin∠DAB1的值；

（3）如果题设中“BE=2CE”改为“=x”，其它条件都不变，试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围（只要写出结论，不需写出解题过程）．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某地的一种绿色蔬菜,在市场上若直接销售,每吨利润为1000元,经粗加工后销售,每吨利润4000元,经精加工后销售, 每吨利润为7000元.当地一家公司现有这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨, 如果对蔬菜进行精加工,每天可加工6吨,但每天两种方式不能同时进行.受季节等条件的限制,必须用15天时间将这批蔬菜全部销售或加工完毕.为此,公司研制了三种方案:

方案1:将蔬菜全部进行粗加工;

方案2:尽可能地对蔬菜进行精加工,没来得及加工的蔬菜,在市场上直接出售;

方案3:将一部分蔬菜进行精加工, 其余蔬菜进行粗加工,并刚好15天完成.

如果你是公司经理,你会选择哪一种方案? 请通过计算说明.

查看答案和解析>>

科目：初中数学 来源： 题型：