
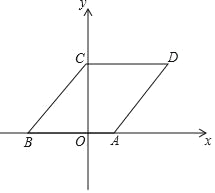
【题目】如图,在平面直角坐标系中,菱形ABCD的边AB在x轴上,点B坐标(﹣3,0),点C在y轴正半轴上,且sin∠CBO=![]() ,点P从原点O出发,以每秒一个单位长度的速度沿x轴正方向移动,移动时间为t(0≤t≤5)秒,过点P作平行于y轴的直线l,直线l扫过四边形OCDA的面积为S.
,点P从原点O出发,以每秒一个单位长度的速度沿x轴正方向移动,移动时间为t(0≤t≤5)秒,过点P作平行于y轴的直线l,直线l扫过四边形OCDA的面积为S.
(1)求点D坐标.
(2)求S关于t的函数关系式.
(3)在直线l移动过程中,l上是否存在一点Q,使以B、C、Q为顶点的三角形是等腰直角三角形?若存在,直接写出Q点的坐标;若不存在,请说明理由.
【答案】(1)D(5,4);(2)见解析;(3)点Q坐标为(![]() ,
,![]() )或(4,1)或(1,﹣3).
)或(4,1)或(1,﹣3).
【解析】
(1)在Rt△BOC中,OB=3,sin∠CBO=![]() ,设CO=4k,BC=5k,根据BC2=CO2+OB2,可得25k2=16k2+9,推出k=1或﹣1(舍弃),求出菱形的边长即可解决问题;
,设CO=4k,BC=5k,根据BC2=CO2+OB2,可得25k2=16k2+9,推出k=1或﹣1(舍弃),求出菱形的边长即可解决问题;
(2)①如图1中,当0≤t≤2时,直线l扫过的图象是四边形CCQP,S=4t;②如图2中,当2<t≤5时,直线l扫过的图形是五边形OCQTA.分别求解即可解决问题;
(3)画出符合条件的图形,分三种情形分别求解即可解决问题;
(1)在Rt△BOC中,OB=3,sin∠CBO=![]() ,设CO=4k,BC=5k,
,设CO=4k,BC=5k,
∵BC2=CO2+OB2,
∴25k2=16k2+9,
∴k=1或﹣1(舍去),
BC=5,OC=4,
∵四边形ABCD是菱形,
∴CD=BC=5,
∴D(5,4);
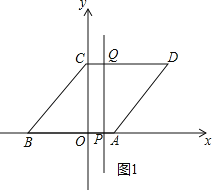
(2)①如图1中,当0≤t≤2时,直线l扫过的图象是四边形CCQP,S=4t.
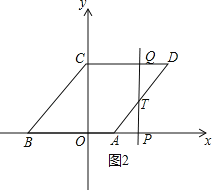
②如图2中,当2<t≤5时,直线l扫过的图形是五边形OCQTA.
S=S梯形OCDA﹣S△DQT=![]() ×(2+5)×4﹣
×(2+5)×4﹣![]() ×(5﹣t)×
×(5﹣t)×![]() (5﹣t)=﹣
(5﹣t)=﹣![]() t2+
t2+![]() t﹣
t﹣![]() ,
,
∴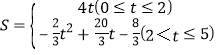 ;
;
(3)如图3中,①当QB=QC,∠BQC=90°,Q(![]() ,
,![]() );
);
②当BC=CQ′,∠BCQ′=90°时,Q′(4,1);
③当BC=BQ″,∠CBQ″=90°时,Q″(1,﹣3);
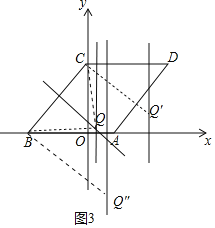
综上所述,满足条件的点Q坐标为(![]() ,
,![]() )或(4,1)或(1,﹣3).
)或(4,1)或(1,﹣3).


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】将![]() 纸片沿
纸片沿![]() 折叠,其中
折叠,其中![]() .
.
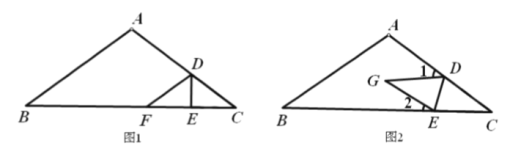
(1)如图1,点![]() 落在
落在![]() 边上的点
边上的点![]() 处,
处,![]() 与
与![]() 是否平行?请说明理由;
是否平行?请说明理由;
(2)如图2,点![]() 落在四边形
落在四边形![]() 内部的点
内部的点![]() 处,探索
处,探索![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校体育组对本校九年级全体同学体育测试情况进行调查,他们随机抽查部分同学体育测试成绩(由高到低分![]() 四个等级),根据调查的数据绘制成如下的条形统计图和扇形统计图.
四个等级),根据调查的数据绘制成如下的条形统计图和扇形统计图.
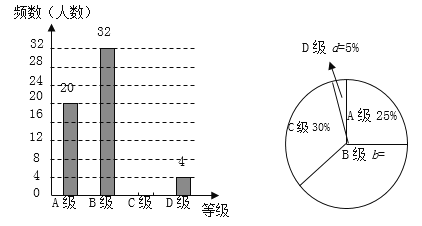
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)该校体育组共抽查了多少名同学的体育测试成绩?扇形统计图中B级所占的百分比b等于多少?
(2)补全条形统计图;
(3)若该校九年级共有200名同学,请估计该校九年级同学体育测试达标(测试成绩C级以上,含C级)约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BP是∠ABC的平分线,AP⊥BP于P,连接PC,若△ABC的面积为1cm2则△PBC的面积为( ).
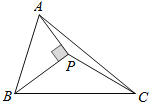
A. 0.4 cm2B. 0.5 cm2
C. 0.6 cm2D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班要购买6副乒乓球拍和![]() 盒(
盒(![]() )乒乓球,甲、乙两家商店定价都为乒乓球拍每副50元,乒乓球每盒10元,现两家商店都搞促销活动,甲店优惠方案是:每买一副乒乓球拍送一盒乒乓球,乙店优惠方案是:按定价的9折出售.
)乒乓球,甲、乙两家商店定价都为乒乓球拍每副50元,乒乓球每盒10元,现两家商店都搞促销活动,甲店优惠方案是:每买一副乒乓球拍送一盒乒乓球,乙店优惠方案是:按定价的9折出售.
(1)用含![]() 的代数式表示:该班在甲店购买时需付款____________元;在乙店购买时需付款____________元,(所填式子需化为最简形式).
的代数式表示:该班在甲店购买时需付款____________元;在乙店购买时需付款____________元,(所填式子需化为最简形式).
(2)当![]() 时,到哪家店子购买比较合算?说明理由.
时,到哪家店子购买比较合算?说明理由.
(3)若要你去甲、乙两家商店购买6副球拍和10盒乒乓球,你最少要付多少钱?并写出你的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
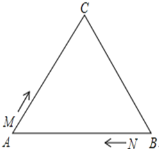
【题目】如图所示,已知△ABC中,AB=AC=BC=10厘米,M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度是1厘米/秒的速度,点N的速度是2厘米/秒,当点N第一次到达B点时,M、N同时停止运动.
(1)M、N同时运动几秒后,M、N两点重合?
(2)M、N同时运动几秒后,可得等边三角形△AMN?
(3)M、N在BC边上运动时,能否得到以MN为底边的等腰△AMN,如果存在,请求出此时M、N运动的时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
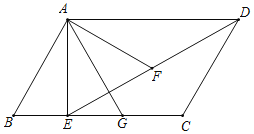
【题目】如图,在平行四边形ABCD中,AE是BC边上的高,点F是DE的中点,AB与AG关于AE对称,AE与AF关于AG对称.
(1)求证:△AEF是等边三角形;
(2)若AB=2,求△AFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
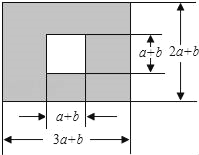
【题目】如图,某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地块,中间是边长为(a+b)米的正方形,规划部门计划将在中间的正方形修建一座雕像,四周的阴影部分进行绿化.
(1)绿化的面积是多少平方米?(用含字母a、b的式子表示)
(2)求出当a=10,b=12时的绿化面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com