
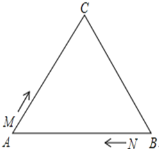
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§“―÷ΣΓςABC÷–Θ§AB=AC=BC=10άεΟΉΘ§MΓΔNΖ÷±π¥”ΒψAΓΔΒψBΆ§ ±≥ωΖΔΘ§―Ί»ΐΫ«–ΈΒΡ±Ώ‘ΥΕ·Θ§“―÷ΣΒψMΒΡΥΌΕ» «1άεΟΉ/ΟκΒΡΥΌΕ»Θ§ΒψNΒΡΥΌΕ» «2άεΟΉ/ΟκΘ§Β±ΒψNΒΎ“Μ¥ΈΒΫ¥οBΒψ ±Θ§MΓΔNΆ§ ±ΆΘ÷Ι‘ΥΕ·Θ°
Θ®1Θ©MΓΔNΆ§ ±‘ΥΕ·ΦΗΟκΚσΘ§MΓΔNΝΫΒψ÷ΊΚœΘΩ
Θ®2Θ©MΓΔNΆ§ ±‘ΥΕ·ΦΗΟκΚσΘ§Ω…ΒΟΒ»±Ώ»ΐΫ«–ΈΓςAMNΘΩ
Θ®3Θ©MΓΔN‘ΎBC±Ώ…œ‘ΥΕ· ±Θ§ΡήΖώΒΟΒΫ“‘MNΈΣΒΉ±ΏΒΡΒ»―ϋΓςAMNΘ§»γΙϊ¥φ‘ΎΘ§«κ«σ≥ω¥Υ ±MΓΔN‘ΥΕ·ΒΡ ±ΦδΘΩ
ΓΨ¥πΑΗΓΩ(1)10Οκ;(2)![]() Οκ;(3)
Οκ;(3)![]() Οκ.
Οκ.
ΓΨΫβΈωΓΩ
Θ®1Θ© Ήœ»…ηΒψMΓΔN‘ΥΕ·xΟκΚσΘ§MΓΔNΝΫΒψ÷ΊΚœΘ§±μ Ψ≥ωMΘ§NΒΡ‘ΥΕ·¬Ζ≥ΧΘ§NΒΡ‘ΥΕ·¬Ζ≥Χ±»MΒΡ‘ΥΕ·¬Ζ≥ΧΕύ10cmΘ§Ν–≥ωΖΫ≥Χ«σΫβΦ¥Ω…ΘΜ
Θ®2Θ©ΗυΨίΧβ“β…ηΒψMΓΔN‘ΥΕ·tΟκΚσΘ§Ω…ΒΟΒΫΒ»±Ώ»ΐΫ«–ΈΓςAMNΘ§»ΜΚσ±μ Ψ≥ωAMΘ§ANΒΡ≥ΛΘ§”…”ΎΓœAΒ»”Ύ60ΓψΘ§Υυ“‘÷Μ“ΣAM=AN»ΐΫ«–ΈANMΨΆ «Β»±Ώ»ΐΫ«–ΈΘΜ
Θ®3Θ© Ήœ»ΦΌ…ηΓςAMN «Β»―ϋ»ΐΫ«–ΈΘ§Ω…÷Λ≥ωΓςACMΓ’ΓςABNΘ§Ω…ΒΟCM=BNΘ§…η≥ω‘ΥΕ· ±ΦδΘ§±μ Ψ≥ωCMΘ§NBΒΡ≥ΛΘ§Ν–≥ωΖΫ≥ΧΘ§Ω…Ϋβ≥ωΈ¥÷Σ ΐΒΡ
Θ®1Θ©…ηΒψMΓΔN‘ΥΕ·xΟκΚσΘ§MΓΔNΝΫΒψ÷ΊΚœΘ§
x+10=2xΘ§ΫβΒΟx=10ΘΜ
Θ®2Θ©…ηΒψMΓΔN‘ΥΕ·tΟκΚσΘ§Ω…ΒΟΒΫΒ»±Ώ»ΐΫ«–ΈΓςAMNΘ§»γΆΦΔΌΘ§

AM=tΘ§AN=AB®CBN=10®C2tΘ§
ΓΏ»ΐΫ«–ΈΓςAMN «Β»±Ώ»ΐΫ«–ΈΘ§
Γύt=10®C2tΘ§ΫβΒΟt=![]() Θ§
Θ§
ΓύΒψMΓΔN‘ΥΕ·![]() ΟκΚσΘ§Ω…ΒΟΒΫΒ»±Ώ»ΐΫ«–ΈΓςAMNΘ°
ΟκΚσΘ§Ω…ΒΟΒΫΒ»±Ώ»ΐΫ«–ΈΓςAMNΘ°
Θ®3Θ©Β±ΒψMΓΔN‘ΎBC±Ώ…œ‘ΥΕ· ±Θ§Ω…“‘ΒΟΒΫ“‘MNΈΣΒΉ±ΏΒΡΒ»―ϋ»ΐΫ«–ΈΘ§
”…Θ®1Θ©÷Σ10Οκ ±MΓΔNΝΫΒψ÷ΊΚœΘ§«ΓΚΟ‘ΎΒψC¥ΠΘ§
»γΆΦΔΎΘ§ΦΌ…ηΓςAMN «Β»―ϋ»ΐΫ«–ΈΘ§

ΓύAN=AMΘ§ΓύΓœAMN=ΓœANMΘ§ΓύΓœAMC=ΓœANBΘ§
ΓΏAB=BC=ACΘ§ΓύΓςACB «Β»±Ώ»ΐΫ«–ΈΘ§ΓύΓœC=ΓœBΘ§
‘ΎΓςACMΚΆΓςABN÷–Θ§
ΓΏ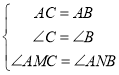 Θ§
Θ§
ΓύΓςACMΓ’ΓςABNΘ®AASΘ©Θ§
ΓύCM=BNΘ§
…ηΒ±ΒψMΓΔN‘ΎBC±Ώ…œ‘ΥΕ· ±Θ§MΓΔN‘ΥΕ·ΒΡ ±ΦδΈΣyΟκ ±Θ§ΓςAMN «Β»―ϋ»ΐΫ«–ΈΘ§
ΓύCM=y®C10Θ§NB=30®C2yΘ§CM=NBΘ§
y®C10=30®C2yΘ§
ΫβΒΟΘΚy=![]() Θ°Ι ΦΌ…η≥…ΝΔΘ°
Θ°Ι ΦΌ…η≥…ΝΔΘ°
ΓύΒ±ΒψMΓΔN‘ΎBC±Ώ…œ‘ΥΕ· ±Θ§ΡήΒΟΒΫ“‘MNΈΣΒΉ±ΏΒΡΒ»―ϋΓςAMNΘ§¥Υ ±MΓΔN‘ΥΕ·ΒΡ ±ΦδΈΣ![]() ΟκΘ°
ΟκΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
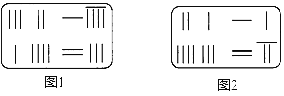
ΓΨΧβΡΩΓΩΓΕΨ≈’¬Υψ θΓΖ «Έ“ΙζΕΪΚΚ≥θΡξ±ύΕ©ΒΡ“Μ≤Ω ΐ―ßΨ≠Βδ÷χΉς.‘ΎΥϋΒΡΓΑΖΫ≥ΧΓ±“Μ’¬άο,“Μ¥ΈΖΫ≥ΧΉι «”…Υψ≥ο≤Φ÷ΟΕχ≥…ΒΡ.ΓΕΨ≈’¬Υψ θΓΖ÷–ΒΡΥψ≥οΆΦ « ζ≈≈ΒΡ,œ÷‘ΎΈ“Ο«Α―ΥϋΗΡΈΣΚα≈≈,»γΆΦ1ΓΔΆΦ2Θ§ΆΦ÷–Ης––¥”ΉσΒΫ”“Ν–≥ωΒΡΥψ≥ο ΐΖ÷±π±μ ΨΈ¥÷Σ ΐ![]() ΒΡœΒ ΐ”κœύ”ΠΒΡ≥Θ ΐœν,Α―ΆΦ1Υυ ΨΒΡΥψ≥οΆΦ”ΟΈ“Ο«œ÷‘ΎΥυ λœΛΒΡΖΫ≥ΧΉι–Έ Ϋ±μ ω≥ωά¥ΨΆ «
ΒΡœΒ ΐ”κœύ”ΠΒΡ≥Θ ΐœν,Α―ΆΦ1Υυ ΨΒΡΥψ≥οΆΦ”ΟΈ“Ο«œ÷‘ΎΥυ λœΛΒΡΖΫ≥ΧΉι–Έ Ϋ±μ ω≥ωά¥ΨΆ «![]()
![]() άύΥΤΒΊ,ΆΦ2Υυ ΨΒΡΥψ≥οΆΦΈ“Ο«Ω…“‘”ΟΖΫ≥ΧΉι–Έ Ϋ±μ ωΈΣ__________.
άύΥΤΒΊ,ΆΦ2Υυ ΨΒΡΥψ≥οΆΦΈ“Ο«Ω…“‘”ΟΖΫ≥ΧΉι–Έ Ϋ±μ ωΈΣ__________.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
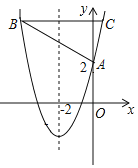
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏy=x2+bx+c”κy÷αΫΜ”ΎΒψAΘ®0Θ§2Θ©Θ§Ε‘≥Τ÷αΈΣ÷±œΏx=©¹2Θ§ΤΫ––”Ύx÷αΒΡ÷±œΏ”κ≈ΉΈοœΏΫΜ”ΎBΓΔCΝΫΒψΘ§ΒψB‘ΎΕ‘≥Τ÷αΉσ≤ύΘ§BC=6Θ°
Θ®1Θ©«σ¥Υ≈ΉΈοœΏΒΡΫβΈω ΫΘ°
Θ®2Θ©ΒψP‘Ύx÷α…œΘ§÷±œΏCPΫΪΓςABCΟφΜΐΖ÷≥…2ΘΚ3ΝΫ≤ΩΖ÷Θ§«κ÷±Ϋ”–¥≥ωPΒψΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈ“Ο«÷ΣΒάΘ§Ψ≠Ιΐ»ΐΫ«–Έ“ΜΕΞΒψΚΆ¥ΥΕΞΒψΥυΕ‘±Ώ…œΒΡ»Έ“β“ΜΒψΒΡ÷±œΏΘ§ΨυΡήΑ―»ΐΫ«–ΈΖ÷Ην≥…ΝΫΗω»ΐΫ«–Έ.
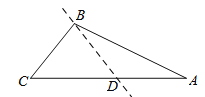
(1)»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœA=25ΓψΘ§ΓœABC=105ΓψΘ§ΙΐBΉς“Μ÷±œΏΫΜAC”ΎDΘ§»τBDΑ―ΓςABCΖ÷Ην≥…ΝΫΗωΒ»―ϋ»ΐΫ«–ΈΘ§‘ρΓœBDAΒΡΕ» ΐ «________ΓψΘΜ
(2)“―÷Σ‘ΎΓςABC÷–Θ§AB=ACΘ§ΙΐΕΞΒψΚΆΕΞΒψΕ‘±Ώ…œ“ΜΒψΒΡ÷±œΏΘ§Α―ΓςABCΖ÷Ην≥…ΝΫΗωΒ»―ϋ»ΐΫ«–ΈΘ§‘ρΓœAΒΡΉν–ΓΕ» ΐΈΣ________Γψ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
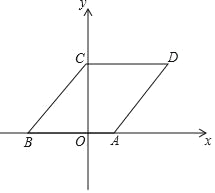
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Νβ–ΈABCDΒΡ±ΏAB‘Ύx÷α…œΘ§ΒψBΉχ±ξΘ®©¹3Θ§0Θ©Θ§ΒψC‘Ύy÷α’ΐΑκ÷α…œΘ§«“sinΓœCBO=![]() Θ§ΒψP¥”‘≠ΒψO≥ωΖΔΘ§“‘ΟΩΟκ“ΜΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―Ίx÷α’ΐΖΫœρ“ΤΕ·Θ§“ΤΕ· ±ΦδΈΣtΘ®0ΓήtΓή5Θ©ΟκΘ§ΙΐΒψPΉςΤΫ––”Ύy÷αΒΡ÷±œΏlΘ§÷±œΏl…®ΙΐΥΡ±Ώ–ΈOCDAΒΡΟφΜΐΈΣSΘ°
Θ§ΒψP¥”‘≠ΒψO≥ωΖΔΘ§“‘ΟΩΟκ“ΜΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―Ίx÷α’ΐΖΫœρ“ΤΕ·Θ§“ΤΕ· ±ΦδΈΣtΘ®0ΓήtΓή5Θ©ΟκΘ§ΙΐΒψPΉςΤΫ––”Ύy÷αΒΡ÷±œΏlΘ§÷±œΏl…®ΙΐΥΡ±Ώ–ΈOCDAΒΡΟφΜΐΈΣSΘ°
Θ®1Θ©«σΒψDΉχ±ξΘ°
Θ®2Θ©«σSΙΊ”ΎtΒΡΚ· ΐΙΊœΒ ΫΘ°
Θ®3Θ©‘Ύ÷±œΏl“ΤΕ·Ιΐ≥Χ÷–Θ§l…œ «Ζώ¥φ‘Ύ“ΜΒψQΘ§ Ι“‘BΓΔCΓΔQΈΣΕΞΒψΒΡ»ΐΫ«–Έ «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§÷±Ϋ”–¥≥ωQΒψΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
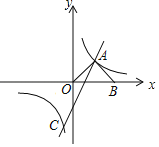
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§÷±œΏy1=2x©¹2”κΥΪ«ζœΏy2=![]() ΫΜ”ΎAΓΔCΝΫΒψΘ§ABΓΆOAΫΜx÷α”ΎΒψBΘ§«“OA=ABΘ°
ΫΜ”ΎAΓΔCΝΫΒψΘ§ABΓΆOAΫΜx÷α”ΎΒψBΘ§«“OA=ABΘ°
Θ®1Θ©«σΥΪ«ζœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©«σΒψCΒΡΉχ±ξΘ§≤Δ÷±Ϋ”–¥≥ωy1ΘΦy2 ±xΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΝΥΫβΡ≥ΙΪΥΨ‘±ΙΛΒΡΡξ ’»κ«ιΩωΘ§ΥφΜζ≥ι≤ιΝΥΙΪΥΨ≤ΩΖ÷‘±ΙΛΡξ ’»κ«ιΩω≤ΔΜφ÷Τ»γΆΦΥυ ΨΆ≥ΦΤΆΦ.
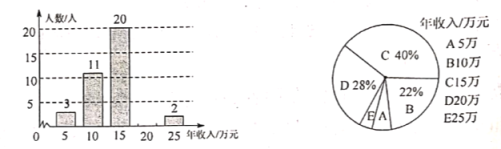
Θ®1Θ©«κΑ¥ΆΦ÷– ΐΨί≤Ι»ΪΧθ–ΈΆΦΘΜ
Θ®2Θ©”…ΆΦΩ…÷Σ‘±ΙΛΡξ ’»κΒΡ÷–ΈΜ ΐ « Θ§÷Ύ ΐ « ΘΜ
Θ®3Θ©ΙάΦΤΗΟΙΪΥΨ‘±ΙΛ»ΥΨυΡξ ’»κ‘ΦΈΣΕύ…Ό‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§‘ΎΓςABC÷–Θ§“―÷ΣΒψDΘ§EΘ§FΖ÷±π «BCΘ§ADΘ§CEΒΡ÷–ΒψΘ§«“SΓςABC=4Θ§‘ρSΓςBEFΒΡΒ»”ΎΘ® Θ©
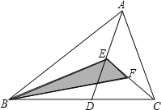
A. ![]() B. 1C. 2D. 3
B. 1C. 2D. 3
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓςABC ÷–Θ§ABΘΫ15Θ§ACΘΫ13Θ§ΗΏ ADΘΫ12Θ§‘ρΓςABC ΒΡ÷ή≥Λ «Θ® Θ©
A. 42B. 32C. 42 Μρ 32D. 42 Μρ 37
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com