
【题目】如图1,在△ABC中,AB=AC,∠ABC=α,D是BC边上一点,以AD为边作△ADE,使AE=AD,∠DAE+∠BAC=180°.
(1)直接写出∠ADE的度数(用含α的式子表示);
(2)以AB,AE为边作平行四边形ABFE,
①如图2,若点F恰好落在DE上,求证:BD=CD;
②如图3,若点F恰好落在BC上,求证:BD=CF.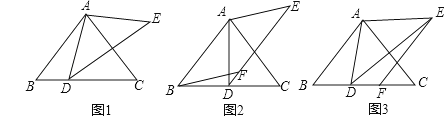
【答案】解:(1)∵在△ABC中,AB=AC,∠ABC=α,
∴∠BAC=180°﹣2α,
∵∠DAE+∠BAC=180°,
∴∠DAE=2α,
∵AE=AD,
∴∠ADE=90°﹣α;
(2)①证明:∵四边形ABFE是平行四边形,
∴AB∥EF.
∴∠EDC=∠ABC=α,
由(1)知,∠ADE=90°﹣α,
∴∠ADC=∠ADE+∠EDC=90°,
∴AD⊥BC.
∵AB=AC,
∴BD=CD;
②证明:∵AB=AC,∠ABC=α,
∴∠C=∠B=α.
∵四边形ABFE是平行四边形,
∴AE∥BF,AE=BF.
∴∠EAC=∠C=α,
由(1)知,∠DAE=2α,
∴∠DAC=α,
∴∠DAC=∠C.
∴AD=CD.
∵AD=AE=BF,
∴BF=CD.
∴BD=CF.
【解析】(1)由在△ABC中,AB=AC,∠ABC=α,可求得∠BAC=180°﹣2α,又由AE=AD,∠DAE+∠BAC=180°,可求得∠DAE=2α,继而求得∠ADE的度数;
(2)①由四边形ABFE是平行四边形,易得∠EDC=∠ABC=α,则可得∠ADC=∠ADE+∠EDC=90°,证得AD⊥BC,又由AB=AC,根据三线合一的性质,即可证得结论;
②由在△ABC中,AB=AC,∠ABC=α,可得∠B=∠C=α,四边形ABFE是平行四边形,可得AE∥BF,AE=BF.即可证得:∠EAC=∠C=α,又由(1)可证得AD=CD,又由AD=AE=BF,证得结论.
【考点精析】本题主要考查了平行四边形的判定与性质的相关知识点,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】江苏卫视《最强大脑》曾播出一期“辨脸识人”节目,参赛选手以家庭为单位,每组家庭由爸爸妈妈和宝宝3人组成,爸爸、妈妈和宝宝分散在三块区域,选手需在宝宝中选一个宝宝,然后分别在爸爸区域和妈妈区域中正确找出这个宝宝的父母,不考虑其他因素,仅从数学角度思考,已知在某分期比赛中有A、B、C三组家庭进行比赛:
(1)选手选择A组家庭的宝宝,在妈妈区域中正确找出其妈妈的概率为 ;
(2)如果任选一个宝宝(假如选A组家庭),通过列表或树状图的方法,求选手至少正确找对宝宝父母其中一人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把多项式x3-xy2+x2y+x4-3按x的降幂排列是( )
A.x4+x3+x2y-3-xy2
B.-xy2+x2y+x4+x3-3
C.-3-xy2+x2y+x3+x4
D.x4+x3+x2y-xy2-3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为1的等边三角形,取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的周长记作C1;取BE中点E1 , 作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1 , 它的周长记作C2 . 照此规律作下去,则C2015= 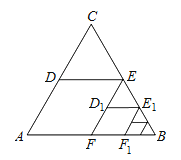
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在学军活动中,一学生连续打靶5次,命中的环数如下:0,2,5,2,7这组数据的中位数与众数分别是(单位:环)( )
A.2,2B.5,2C.5,7D.2,7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=mx2-6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我县九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段统计如表:
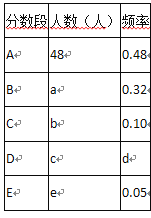
根据上面提供的信息,回答下列问题:
(1)在统计表中,a的值为________,c的值为________;
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数”.请问甲同学体育成绩应在什么分数段内?________(填相应分数段的字母);
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com