
【题目】已知,如图,直线y=![]() x4与x轴,y轴分别交于B、A,将该直线绕A点顺时针旋转α,且tanα=
x4与x轴,y轴分别交于B、A,将该直线绕A点顺时针旋转α,且tanα=![]() ,旋转后与x轴交于C点.
,旋转后与x轴交于C点.
(1)求A、B、C的坐标;
(2)在x轴上找一点P,使有一动点能在最短的时间内从点A出发,沿着A-P-C的 运动到达C点,并且在AP上以每秒2个单位的速度移动,在PC上以每秒![]() 个单位移动,试用尺规作图找到P点的位置(不写作法,保留作图痕迹),并求出所用的最短时间t.
个单位移动,试用尺规作图找到P点的位置(不写作法,保留作图痕迹),并求出所用的最短时间t.

【答案】(1)A(0,4),B(8,0),C(18,0) ;
(2)作图见解析,t=![]()
【解析】试题分析:(1)过B作BD⊥AB交AC于D,过D作DE⊥x轴于E,则△AOB∽△BED,得到![]() =
=![]() =
=![]() ,求出点D坐标,求出AC的解析式即可求出点C坐标.
,求出点D坐标,求出AC的解析式即可求出点C坐标.
(2)过点(0,4)作AC的垂线垂足为Q,该垂线与x轴的交点即为P点.设点F(0,4),则A、F关于x轴对称,所以AP=FP,首先证明t=![]() ,由此推出点P就是所求的点,此时动点能在最短的时间内从点A出发,沿着A-P-C的运动到达C点,求出FQ的长即可解决问题.
,由此推出点P就是所求的点,此时动点能在最短的时间内从点A出发,沿着A-P-C的运动到达C点,求出FQ的长即可解决问题.
试题解析:(1)∵直线y=![]() x4与x轴,y轴分别交于B、A,
x4与x轴,y轴分别交于B、A,
∴A(0,4),B(8,0),
过B作BD⊥AB交AC于D,过D作DE⊥x轴于E,
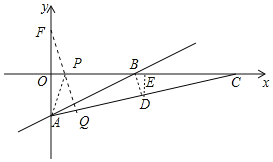
则△AOB∽△BED
∴![]() =
=![]() =
=![]() ,
,
∵OA=4,OB=8,∠BAD=α,tanα=![]() =
=![]() ,
,
∴BE=1,DE=2
∴D(9,2)
∴直线AC解析式为y=![]() x4
x4
∴C(18,0).
(2)过点(0,4)作AC的垂线垂足为Q,该垂线与x轴的交点即为P点。
设点F(0,4),则A.F关于x轴对称,所以AP=FP,
S△ACF=![]() AFOC=
AFOC=![]() ACFQ,AF=8,OC=18,AC=
ACFQ,AF=8,OC=18,AC=![]() =
=![]() =
=![]() ,
,
∴FQ=![]() ,
,
∵△CQP∽△COA,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴t=![]() =
=![]() ,
,
∵FQ是垂线段,
∴点P就是所求的点,此时动点能在最短的时间内从点A出发,沿着APC的运动到达C点,
∴t=![]()


科目:初中数学 来源: 题型:
【题目】如图:在△ABC中点D、E分别在边AC、AB上,BD和CE相交于点O,有下面三个条件:①∠EBO=∠DCO,②BE=CD,③OB=OC.
(1)上述三个条件中,由哪两个条件可以判定出AB=AC.
(2)选择(1)中的一种情形,写出证明的过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在显微镜下,一种细菌的形状可以近似地看成圆,它的半径约为0.00000063m,这个数据用科学记数法表示为( )
A.0.63×10﹣6m
B.6.3×10﹣7m
C.6.3×10﹣8m
D.63×10﹣8m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在平行四边形ABCD中,AE是BC边上的高,将△ABE沿BC方向平移,使点E与点C重合,得△GFC.

(1)求证:BE=DG;
(2)若∠B=60°,当BC= AB时,四边形ABFG是菱形;
(3)若∠B=60°,当BC= AB时,四边形AECG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适宜采用普查方式的是( )
A. 了解一批圆珠笔的寿命 B. 检查一枚用于发射卫星的运载火箭的各零部件
C. 考察人们保护海洋的意识 D. 了解全国九年级学生的身高现状
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(3,![]() ),点B的坐标为(6,0),将△AOB绕点B按顺时针方向旋转一定的角度后得到△A'O'B,点A的对应点A'在x轴上,则点O'的坐标为( )
),点B的坐标为(6,0),将△AOB绕点B按顺时针方向旋转一定的角度后得到△A'O'B,点A的对应点A'在x轴上,则点O'的坐标为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
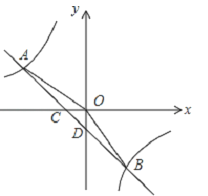
【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=![]() .
.
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com