
【题目】如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)求∠CAM的度数;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.

【答案】(1)30°;(2)答案见解析;(3)∠AOB是定值,∠AOB=60°.
【解析】
(1)根据等边三角形的性质可以直接得出结论;
(2)根据等边三角形的性质就可以得出AC=BC,DC=EC,∠ACB=∠DCE=60°,由等式的性质就可以∠BCE=∠ACD,根据SAS就可以得出△ADC≌△BEC;
(3)分情况讨论:当点D在线段AM上时,如图1,由(2)可知△ACD≌△BCE,就可以求出结论;当点D在线段AM的延长线上时,如图2,可以得出△ACD≌△BCE而有∠CBE=∠CAD=30°而得出结论;当点D在线段MA的延长线上时,如图3,通过得出△ACD≌△BCE同样可以得出结论.
(1)∵△ABC是等边三角形,∴∠BAC=60°.
∵线段AM为BC边上的中线,∴∠CAM![]() ∠BAC,∴∠CAM=∠BAM=30°.
∠BAC,∴∠CAM=∠BAM=30°.
(2)∵△ABC与△DEC都是等边三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∴∠ACD+∠DCB=∠DCB+∠BCE,∴∠ACD=∠BCE.
在△ADC和△BEC中,∵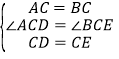 ,∴△ACD≌△BCE(SAS);
,∴△ACD≌△BCE(SAS);
(3)∠AOB是定值,∠AOB=60°.理由如下:
①当点D在线段AM上时,如图1,由(2)可知△ACD≌△BCE,则∠CBE=∠CAD=30°,又∠ABC=60°,∴∠CBE+∠ABC=60°+30°=90°.
∵△ABC是等边三角形,线段AM为BC边上的中线,∴AM平分∠BAC,即![]() ,∴∠BOA=90°﹣30°=60°.
,∴∠BOA=90°﹣30°=60°.
②当点D在线段AM的延长线上时,如图2.
∵△ABC与△DEC都是等边三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∴∠ACB+∠DCB=∠DCB+∠DCE,∴∠ACD=∠BCE.
在△ACD和△BCE中,∵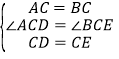 ,∴△ACD≌△BCE(SAS),∴∠CBE=∠CAD=30°.
,∴△ACD≌△BCE(SAS),∴∠CBE=∠CAD=30°.
由(1)得:∠BAM=30°,∴∠BOA=90°﹣30°=60°.
③当点D在线段MA的延长线上时.
∵△ABC与△DEC都是等边三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∴∠ACD+∠ACE=∠BCE+∠ACE=60°,∴∠ACD=∠BCE.
在△ACD和△BCE中,∵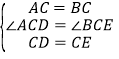 ,∴△ACD≌△BCE(SAS),∴∠CBE=∠CAD.
,∴△ACD≌△BCE(SAS),∴∠CBE=∠CAD.
由(1)得:∠CAM=30°,∴∠CBE=∠CAD=150°,∴∠CBO=30°,∠BAM=30°,∴∠BOA=90°﹣30°=60°.
综上所述:当动点D在直线AM上时,∠AOB是定值,∠AOB=60°.


科目:初中数学 来源: 题型:
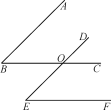
【题目】如图,已知BC,DE相交于点O,给出以下三个判断:①AB∥DE;②BC∥EF;③∠B=∠E,请你以其中两个判断作为题设,另外一个判断作为结论,写出所有的命题,指出这些命题是真命题还是假命题,并选择其中的一个真命题加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠DAE=∠E,∠B=∠D.直线AD与BE平行吗?直线AB与DC平行吗?说明理由(请在下面的解答过程的空格内填空或在括号内填写理由).
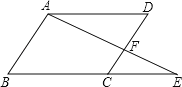
解:直线AD与BE平行,直线AB与DC .
理由如下:
∵∠DAE=∠E,(已知)
∴ ∥ ,(内错角相等,两条直线平行)
∴∠D=∠DCE. (两条直线平行,内错角相等)
又∵∠B=∠D,(已知)
∴∠B= ,(等量代换)
∴ ∥ .(同位角相等,两条直线平行)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪得行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为m.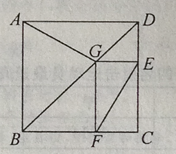
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.若BD=4,DE=7,则线段EC的长为( )

A. 3 B. 4 C. 3.5 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.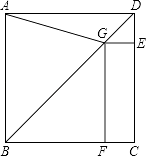
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植树4﹣7颗,活动结束后随机抽查了20名学生每人的植树数量,并分为四种类型,A:4颗;B:5颗;C:6颗;D:7颗.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.
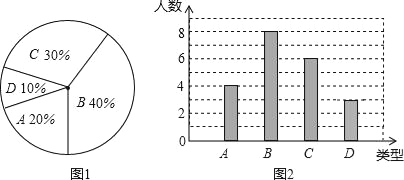
回答下列问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数和中位数;
(3)求这20名学生每人植树量的平均数,并估计这260名学生共植树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某月的日历表,在此目历表上可以用一个“十”字圈出5个数.
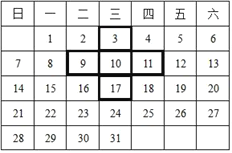
(1)如图中四周的4个数3、9、17、11的和与中间的数10有什么数量关系?
(2)照此方法,任意圈出的5个数是否都具有这样的数量关系?请通过整式的运算说明理由.
(3)用(2)的结论说明圈出的5个数的和能否等于125?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com