
【题目】已知:如图,∠DAE=∠E,∠B=∠D.直线AD与BE平行吗?直线AB与DC平行吗?说明理由(请在下面的解答过程的空格内填空或在括号内填写理由).
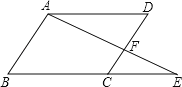
解:直线AD与BE平行,直线AB与DC .
理由如下:
∵∠DAE=∠E,(已知)
∴ ∥ ,(内错角相等,两条直线平行)
∴∠D=∠DCE. (两条直线平行,内错角相等)
又∵∠B=∠D,(已知)
∴∠B= ,(等量代换)
∴ ∥ .(同位角相等,两条直线平行)
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y= ![]() x的图象与反比例函数y=
x的图象与反比例函数y= ![]() 的图象交于A(a,﹣2),B两点.
的图象交于A(a,﹣2),B两点. 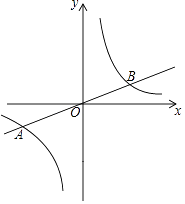
(1)求反比例函数的表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(3,2).点D、E分别在AB、BC边上,BD=BE=1.沿直线DE将△BDE翻折,点B落在点B′处.则点B′的坐标为_____.
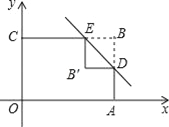
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,已知点
中,已知点 ![]() ,
, ![]() .若平移点
.若平移点 ![]() 到点
到点 ![]() ,使以点
,使以点 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为顶点的四边形是菱形,则正确的平移方法是( )
为顶点的四边形是菱形,则正确的平移方法是( )
A.向左平移1个单位,再向下平移1个单位
B.向左平移 ![]() 个单位,再向上平移1个单位
个单位,再向上平移1个单位
C.向右平移 ![]() 个单位,再向上平移1个单位
个单位,再向上平移1个单位
D.向右平移1个单位,再向上平移1个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )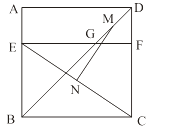
A.3
B.![]()
C.![]()
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y= ![]() (k≠0)的图象恰好经过点A′,B,则k的值为 .
(k≠0)的图象恰好经过点A′,B,则k的值为 . 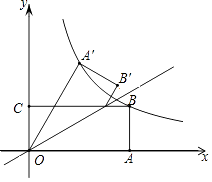
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)求∠CAM的度数;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的有( )
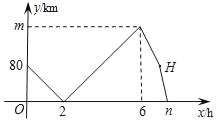
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋中有除颜色外其他完全相同的3个球,每次从袋中摸出一个球,记下颜色后放回搅匀再摸,在摸球试验中得到下表中部分数据:
摸球 总次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
摸到黄球的次数 | 14 | 23 | 38 | 52 | 67 | 86 | 97 | 111 | 120 | 136 |
摸到黄球的频率 | 35% | 32% | 33% | 35% | 35% |
(1)请将上表补充完整(结果精确到1%);
(2)制作折线统计图表示摸到黄球的频率的变化情况;
(3)估计从袋中摸出一个球是黄球的概率是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com