
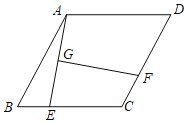
【题目】如图,四边形ABCD为菱形,∠D=60°,AB=4,E为边BC上的动点,连接AE,作AE的垂直平分线GF交直线CD于F点,垂足为点G,则线段GF的最小值为____________.
【答案】3
【解析】
作辅助线,构建三角形全等,证明Rt△AFM≌Rt△EFN(HL),得∠AFM=∠EFN,再证明△AEF是等边三角形,计算FG=![]() AG=
AG=![]() AE,确认当AE⊥BC时,即AE=2
AE,确认当AE⊥BC时,即AE=2![]() 时,FG最小.
时,FG最小.
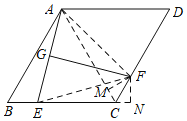
解:连接AC,过点F作FM⊥AC于,作FN⊥BC于N,连接AF、EF,
∵四边形ABCD是菱形,且∠D=60°,
∴∠B=∠D=60°,AD∥BC,
∴∠FCN=∠D=60°=∠FCM,
∴FM=FN,
∵FG垂直平分AE,
∴AF=EF,
∴Rt△AFM≌Rt△EFN(HL),
∴∠AFM=∠EFN,
∴∠AFE=∠MFN,
∵∠FMC=∠FNC=90°,∠MCN=120°,
∴∠MFN=60°,
∴∠AFE=60°,
∴△AEF是等边三角形,
∴FG=![]() AG=
AG=![]() AE,
AE,
∴当AE⊥BC时,Rt△ABE中,∠B=60°,
∴∠BAE=30°,
∵AB=4,
∴BE=2,AE=2![]() ,
,
∴当AE⊥BC时,即AE=2![]() 时,FG最小,最小为3;
时,FG最小,最小为3;
故答案为:3.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
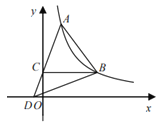
【题目】如图,点A、B都在反比例函数y=![]() (x>0)的图像上,过点B作BC∥x轴交y轴于点C,连接AC并延长交x轴于点D,连接BD,DA=3DC,S△ABD=6.则k的值为_______.
(x>0)的图像上,过点B作BC∥x轴交y轴于点C,连接AC并延长交x轴于点D,连接BD,DA=3DC,S△ABD=6.则k的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化,促进学生全面发展.我市某区教育局在全区中小学开展“书法、武术、黄梅戏进校园”活动。今年3月份,该区某校举行了“黄梅戏”演唱比赛,比赛成绩评定为A,B,C,D,E五个等级,该校部分学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图,请根据图中信息,解答下列问题.

(1)求该校参加本次“黄梅戏”演唱比赛的学生人数;
(2)求扇形统计图B等级所对应扇形的圆心角度数;
(3)已知A等级的4名学生中有1名男生,3名女生,现从中任意选取2名学生作为全校训练的示范者,请你用列表法或画树状图的方法,求出恰好选1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武胜县白坪—飞龙乡村旅游度假村橙海阳光景点组织![]() 辆汽车装运完
辆汽车装运完![]() 三种脐橙共
三种脐橙共![]() 吨到外地销售.按计划,
吨到外地销售.按计划,![]() 辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满.根据下表提供的信息,解答以下问题:
辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满.根据下表提供的信息,解答以下问题:
脐橙品种 |
|
|
|
每辆汽车运载量(吨) |
|
|
|
每吨脐橙获得(元) |
|
|
|
![]() 设装运
设装运![]() 种脐橙的车辆数为
种脐橙的车辆数为![]() ,装运
,装运![]() 种脐橙的车辆数为
种脐橙的车辆数为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 如果装运每种脐橙的车辆数都不少于
如果装运每种脐橙的车辆数都不少于![]() 辆,那么车辆的安排方案有几种?
辆,那么车辆的安排方案有几种?
![]() 设销售利润为
设销售利润为![]() (元),求
(元),求![]() 与
与![]() 之间的函数关系式;若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
之间的函数关系式;若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:已知Rt△ABC的周长为30,斜边长c=13,求△ABC的面积.、
解法展示:设Rt△ABC的两直角边长分别为a,b,则a+b+c=①______,
因为c=13,所以a+b=②______,
所以(a+b)2=③______,所以a2+ b2+④_____=289.
因为a2+b2=c2,所以c2+2ab=289,
所以⑤______+2ab=289,所以ab=⑥______(第1步),
所以△ABC的面积=![]() ab=
ab=![]() ×⑦______=⑧______(第2步).
×⑦______=⑧______(第2步).
合作探究:(1)对解法展示进行填空.
(2)上述解题过程中,由第1步到第2步体现出来的数学思想是______(填序号).
①整体思想;②数形结合思想;③分类讨论思想.
方法迁移:
(3)已知一直角三角形的面积为24,斜边长为10,求这个直角三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
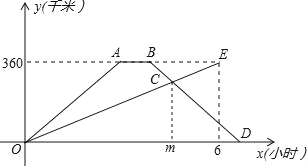
【题目】(8分)快、慢两车分别从相距360千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地,快、慢两车距各自出发地的路程y(千米)与出发后所用的时间x(小时)的关系如图.
请结合图象信息解答下列问题:
(1)慢车的速度是 千米/小时,快车的速度是 千米/小时;
(2)求m的值,并指出点C的实际意义是什么?
(3)在快车按原路原速返回的过程中,快、慢两车相距的路程为150千米时,慢车行驶了多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
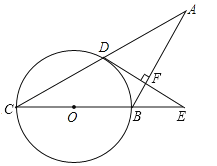
【题目】如图,在等腰△ABC中,AB=BC,以BC为直径的⊙O与AC相交于点D,过点D作DE⊥AB交CB延长线于点E,垂足为点F.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径R=5,tanC=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com