
ΓΨΧβΡΩΓΩΈδ ΛœΊΑΉΤΚΓΣΖ…Νζœγ¥ε¬Ο”ΈΕ»ΦΌ¥ε≥»ΚΘ―τΙβΨΑΒψΉι÷·![]() ΝΨΤϊ≥ΒΉΑ‘ΥΆξ
ΝΨΤϊ≥ΒΉΑ‘ΥΆξ![]() »ΐ÷÷Τξ≥»Ι≤
»ΐ÷÷Τξ≥»Ι≤![]() Ε÷ΒΫΆβΒΊœζ έ.Α¥ΦΤΜ°Θ§
Ε÷ΒΫΆβΒΊœζ έ.Α¥ΦΤΜ°Θ§![]() ΝΨΤϊ≥ΒΕΦ“ΣΉΑ‘ΥΘ§ΟΩΝΨΤϊ≥Β÷ΜΡήΉΑ‘ΥΆ§“Μ÷÷Τξ≥»Θ§«“±Ί–κΉΑ¬ζ.ΗυΨίœ¬±μΧαΙ©ΒΡ–≈œΔΘ§Ϋβ¥π“‘œ¬Έ ΧβΘΚ
ΝΨΤϊ≥ΒΕΦ“ΣΉΑ‘ΥΘ§ΟΩΝΨΤϊ≥Β÷ΜΡήΉΑ‘ΥΆ§“Μ÷÷Τξ≥»Θ§«“±Ί–κΉΑ¬ζ.ΗυΨίœ¬±μΧαΙ©ΒΡ–≈œΔΘ§Ϋβ¥π“‘œ¬Έ ΧβΘΚ
Τξ≥»ΤΖ÷÷ |
|
|
|
ΟΩΝΨΤϊ≥Β‘Υ‘ΊΝΩΘ®Ε÷Θ© |
|
|
|
ΟΩΕ÷Τξ≥»ΜώΒΟΘ®‘ΣΘ© |
|
|
|
![]() …ηΉΑ‘Υ
…ηΉΑ‘Υ![]() ÷÷Τξ≥»ΒΡ≥ΒΝΨ ΐΈΣ
÷÷Τξ≥»ΒΡ≥ΒΝΨ ΐΈΣ![]() Θ§ΉΑ‘Υ
Θ§ΉΑ‘Υ![]() ÷÷Τξ≥»ΒΡ≥ΒΝΨ ΐΈΣ
÷÷Τξ≥»ΒΡ≥ΒΝΨ ΐΈΣ![]() Θ§«σ
Θ§«σ![]() ”κ
”κ![]() ÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
![]() »γΙϊΉΑ‘ΥΟΩ÷÷Τξ≥»ΒΡ≥ΒΝΨ ΐΕΦ≤Μ…Ό”Ύ
»γΙϊΉΑ‘ΥΟΩ÷÷Τξ≥»ΒΡ≥ΒΝΨ ΐΕΦ≤Μ…Ό”Ύ![]() ΝΨΘ§Ρ«Ο¥≥ΒΝΨΒΡΑ≤≈≈ΖΫΑΗ”–ΦΗ÷÷ΘΩ
ΝΨΘ§Ρ«Ο¥≥ΒΝΨΒΡΑ≤≈≈ΖΫΑΗ”–ΦΗ÷÷ΘΩ
![]() …ηœζ έάϊ»σΈΣ
…ηœζ έάϊ»σΈΣ![]() Θ®‘ΣΘ©Θ§«σ
Θ®‘ΣΘ©Θ§«σ![]() ”κ
”κ![]() ÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ»τ“Σ Ι¥Υ¥Έœζ έΜώάϊΉν¥σΘ§”Π≤…”ΟΡΡ÷÷Α≤≈≈ΖΫΑΗΘΩ≤Δ«σ≥ωΉν¥σάϊ»σΒΡ÷Β.
÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ»τ“Σ Ι¥Υ¥Έœζ έΜώάϊΉν¥σΘ§”Π≤…”ΟΡΡ÷÷Α≤≈≈ΖΫΑΗΘΩ≤Δ«σ≥ωΉν¥σάϊ»σΒΡ÷Β.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©5÷÷ΘΜΘ®3Θ©ΉΑ‘Υ
ΘΜΘ®2Θ©5÷÷ΘΜΘ®3Θ©ΉΑ‘Υ![]() ÷÷Τξ≥»
÷÷Τξ≥»![]() ≥ΒΘ§
≥ΒΘ§![]() ÷÷Τξ≥»
÷÷Τξ≥»![]() ≥ΒΘ§
≥ΒΘ§![]() ÷÷Τξ≥»
÷÷Τξ≥»![]() ≥Β ±Θ§ΜώάϊΉν¥σΘ§Ήν¥σάϊ»σΈΣ
≥Β ±Θ§ΜώάϊΉν¥σΘ§Ήν¥σάϊ»σΈΣ![]() ‘Σ.
‘Σ.
ΓΨΫβΈωΓΩ
(1)άϊ”ΟΓΑ≥ΒΝΨ ΐ÷°ΚΆ=20Γ±’βΗωΒ»ΝΩΙΊœΒΫχ––Ν– ΫΦ¥Ω…ΘΜ
(2)ΙΊœΒ ΫΈΣΘΚΉΑ‘ΥΟΩ÷÷Τξ≥»ΒΡ≥ΒΝΨ ΐΓί4ΘΜ
(3)Ήήάϊ»σΈΣΘΚΉΑ‘ΥA÷÷Τξ≥»ΒΡ≥ΒΝΨ ΐΓΝ6ΓΝ1200+ΉΑ‘ΥB÷÷Τξ≥»ΒΡ≥ΒΝΨ ΐΓΝ5ΓΝ1600+ΉΑ‘ΥC÷÷Τξ≥»ΒΡ≥ΒΝΨ ΐΓΝ4ΓΝ1000Θ§»ΜΚσΑ¥xΒΡ»Γ÷Βά¥≈–Ε®Θ°
ΫβΘΚΘ®1Θ©ΗυΨίΧβ“βΘ§ΉΑ‘Υ![]() ÷÷Τξ≥»ΒΡ≥ΒΝΨ ΐΈΣ
÷÷Τξ≥»ΒΡ≥ΒΝΨ ΐΈΣ![]() Θ§ΉΑ‘Υ
Θ§ΉΑ‘Υ![]() ÷÷Τξ≥»ΒΡ≥ΒΝΨ ΐΈΣ
÷÷Τξ≥»ΒΡ≥ΒΝΨ ΐΈΣ![]() Θ§Ρ«Ο¥ΉΑ‘Υ
Θ§Ρ«Ο¥ΉΑ‘Υ![]() ÷÷Τξ≥»ΒΡ≥ΒΝΨ ΐΈΣ
÷÷Τξ≥»ΒΡ≥ΒΝΨ ΐΈΣ![]() Θ§
Θ§
‘ρ”–ΘΚ![]() Θ§Φ¥ΘΚ
Θ§Φ¥ΘΚ![]()
Θ®2Θ©”…![]() ÷ΣΘ§ΉΑ‘Υ
÷ΣΘ§ΉΑ‘Υ![]() »ΐ÷÷Τξ≥»ΒΡ≥ΒΝΨ ΐΖ÷±πΈΣ
»ΐ÷÷Τξ≥»ΒΡ≥ΒΝΨ ΐΖ÷±πΈΣ![]()
”…Χβ“βΒΟΘΚ![]()
ΫβΒΟ![]() Θ§
Θ§
“ρΈΣ![]() ΈΣ’ϊ ΐΘ§
ΈΣ’ϊ ΐΘ§
Υυ“‘![]() ΒΡ÷ΒΈΣ
ΒΡ÷ΒΈΣ![]() Θ§Υυ“‘Α≤≈≈ΖΫΑΗΙ≤”–
Θ§Υυ“‘Α≤≈≈ΖΫΑΗΙ≤”–![]() ÷÷.
÷÷.
Θ®3Θ©![]()
![]()
![]() ΒΡ÷ΒΥφ
ΒΡ÷ΒΥφ![]() ΒΡ‘ω¥σΕχΦθ–Γ
ΒΡ‘ω¥σΕχΦθ–Γ
“Σ Ι![]() άϊ»σΉν¥σΘ§‘ρ
άϊ»σΉν¥σΘ§‘ρ![]() Θ§
Θ§
Ι ―ΓΖΫΑΗΈΣΘΚΉΑ‘Υ![]() ÷÷Τξ≥»
÷÷Τξ≥»![]() ≥ΒΘ§
≥ΒΘ§![]() ÷÷Τξ≥»
÷÷Τξ≥»![]() ≥ΒΘ§
≥ΒΘ§![]() ÷÷Τξ≥»
÷÷Τξ≥»![]() ≥Β.
≥Β.
![]() Θ®‘ΣΘ©
Θ®‘ΣΘ©
¥πΘΚΒ±ΉΑ‘Υ![]() ÷÷Τξ≥»
÷÷Τξ≥»![]() ≥ΒΘ§
≥ΒΘ§![]() ÷÷Τξ≥»
÷÷Τξ≥»![]() ≥ΒΘ§
≥ΒΘ§![]() ÷÷Τξ≥»
÷÷Τξ≥»![]() ≥Β ±Θ§ΜώάϊΉν¥σΘ§Ήν¥σάϊ»σΈΣ
≥Β ±Θ§ΜώάϊΉν¥σΘ§Ήν¥σάϊ»σΈΣ![]() ‘Σ.
‘Σ.
Ι ¥πΑΗΈΣΘΚΘ®1Θ©![]() ΘΜΘ®2Θ©5÷÷ΘΜΘ®3Θ©ΉΑ‘Υ
ΘΜΘ®2Θ©5÷÷ΘΜΘ®3Θ©ΉΑ‘Υ![]() ÷÷Τξ≥»
÷÷Τξ≥»![]() ≥ΒΘ§
≥ΒΘ§![]() ÷÷Τξ≥»
÷÷Τξ≥»![]() ≥ΒΘ§
≥ΒΘ§![]() ÷÷Τξ≥»
÷÷Τξ≥»![]() ≥Β ±Θ§ΜώάϊΉν¥σΘ§Ήν¥σάϊ»σΈΣ
≥Β ±Θ§ΜώάϊΉν¥σΘ§Ήν¥σάϊ»σΈΣ![]() ‘Σ.
‘Σ.


 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§÷±œΏ![]() ”κ
”κ![]() ÷αΓΔ
÷αΓΔ![]() ÷αΖ÷±πΫΜ”ΎΒψ
÷αΖ÷±πΫΜ”ΎΒψ![]() ΓΔ
ΓΔ![]() Θ§Ε·Βψ
Θ§Ε·Βψ![]() ¥”Βψ
¥”Βψ![]() ≥ωΖΔΘ§―Ί
≥ωΖΔΘ§―Ί![]() ÷αΗΚΖΫœρ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘ΥΕ·Θ§Ά§ ±Ε·Βψ
÷αΗΚΖΫœρ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘ΥΕ·Θ§Ά§ ±Ε·Βψ![]() ¥”Βψ
¥”Βψ![]() ≥ωΖΔΘ§―Ί…δœΏ
≥ωΖΔΘ§―Ί…δœΏ![]() ΖΫœρ“‘ΟΩΟκ2ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘ΥΕ·Θ§ΙΐΒψ
ΖΫœρ“‘ΟΩΟκ2ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘ΥΕ·Θ§ΙΐΒψ![]() Ής
Ής![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() ΓΔ
ΓΔ![]() Θ§“‘
Θ§“‘![]() ΓΔ
ΓΔ![]() ΈΣΝΎ±ΏΙΙ‘λΤΫ––ΥΡ±Ώ–Έ
ΈΣΝΎ±ΏΙΙ‘λΤΫ––ΥΡ±Ώ–Έ![]() Θ§…ηΒψ
Θ§…ηΒψ![]() ‘ΥΕ·ΒΡ ±ΦδΈΣ
‘ΥΕ·ΒΡ ±ΦδΈΣ![]() s.
s.
Θ®1Θ©Β±Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œ ±Θ§”ΟΚ§
…œ ±Θ§”ΟΚ§![]() ΒΡ¥ζ ΐ Ϋ±μ Ψ
ΒΡ¥ζ ΐ Ϋ±μ Ψ![]() ΓΔ
ΓΔ![]() ΒΡ≥Λ.
ΒΡ≥Λ.
Θ®2Θ©‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§ΔΌΒ±Βψ![]() ¬δ‘Ύ
¬δ‘Ύ![]() ÷α…œ ±Θ§«σ≥ω¬ζΉψΧθΦΰΒΡ
÷α…œ ±Θ§«σ≥ω¬ζΉψΧθΦΰΒΡ![]() ΒΡ÷Β;ΔΎΒ±Βψ
ΒΡ÷Β;ΔΎΒ±Βψ![]() ¬δ‘Ύ
¬δ‘Ύ![]() ΡΎ≤Ω(≤ΜΑϋά®±ΏΫγ) ±Θ§÷±Ϋ”–¥≥ω
ΡΎ≤Ω(≤ΜΑϋά®±ΏΫγ) ±Θ§÷±Ϋ”–¥≥ω![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
Θ®3Θ©ΉςΒψ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ÷αΒΡΕ‘≥ΤΒψ
÷αΒΡΕ‘≥ΤΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§ «Ζώ¥φ‘ΎΡ≥ ±ΩΧ ΙΙΐ
Θ§‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§ «Ζώ¥φ‘ΎΡ≥ ±ΩΧ ΙΙΐ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() »ΐΒψΒΡ‘≤”κ
»ΐΒψΒΡ‘≤”κ![]() »ΐ±Ώ÷–ΒΡ“ΜΧθ±Ώœύ«–?»τ¥φ‘ΎΘ§«κ«σ≥ω
»ΐ±Ώ÷–ΒΡ“ΜΧθ±Ώœύ«–?»τ¥φ‘ΎΘ§«κ«σ≥ω![]() ΒΡ÷Β;»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΒΡ÷Β;»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
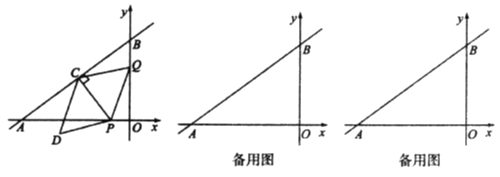
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§’ΐΖΫ–ΈOABCΒΡΕΞΒψAΘ§CΖ÷±π‘Ύx÷αΘ§y÷α…œΘ§OA=3Θ°
Θ®1Θ©«σ÷±œΏOBΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©»τ÷±œΏy=x+b”κΗΟ’ΐΖΫ–Έ”–ΝΫΗωΙΪΙ≤ΒψΘ§«κ÷±Ϋ”–¥≥ωbΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
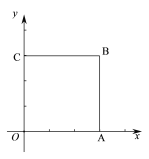
ΓΨΧβΡΩΓΩ»γΆΦ,‘Ύ ΐ÷α…œ”–AΓΔBΝΫΒψ,Υυ±μ ΨΒΡ ΐΖ÷±πΈΣaΓΔa+4,AΒψ“‘ΟΩΟκ3ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρ’ΐΖΫœρ‘ΥΕ·,Ά§ ±BΒψ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»“≤œρ’ΐΖΫœρ‘ΥΕ·,…η‘ΥΕ· ±ΦδΈΣtΟκ.
![]()
(1)‘ΥΕ·«ΑœΏΕΈABΒΡ≥ΛΈΣ ,tΟκΚσ,AΒψ‘ΥΕ·ΒΡΨύάκΩ…±μ ΨΈΣ Θ§ BΒψ‘ΥΕ·ΨύάκΩ…±μ ΨΈΣ
(2)Β±tΈΣΚΈ÷Β ±,AΓΔBΝΫΒψ÷ΊΚœ,≤Δ«σ≥ω¥Υ ±AΒψΥυ±μ ΨΒΡ ΐ(”ΟΚ§”–aΒΡ ΫΉ”±μ Ψ);
(3)‘Ύ…œ ω‘ΥΕ·ΒΡΙΐ≥Χ÷–,»τPΈΣœΏΕΈABΒΡ÷–Βψ,OΈΣ ΐ÷αΒΡ‘≠Βψ,Β±a=-8 ±, «Ζώ¥φ‘Ύ’β―υΒΡ÷Β, ΙΒΟœΏΕΈPO=5,»τ¥φ‘Ύ,«σ≥ωΖϊΚœΧθΦΰΒΡ÷Β;»τ≤Μ¥φ‘Ύ,«κΥΒΟςάμ”…ΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΫώΡξΓΑΈε“ΜΓ±ΫΎΘ§–ΓΟςΆβ≥ω≈ά…ΫΘ§Υϊ¥”…ΫΫ≈≈άΒΫ…ΫΕΞΒΡΙΐ≥Χ÷–Θ§÷–ΆΨ–ίœΔΝΥ“ΜΕΈ ±ΦδΘ°…ηΥϊ¥”…ΫΫ≈≥ωΖΔΚσΥυ”ΟΒΡ ±ΦδΈΣtΘ®Ζ÷÷”Θ©Θ§ΥυΉΏΒΡ¬Ζ≥ΧΈΣsΘ®ΟΉΘ©Θ§s”κt÷°ΦδΒΡΚ· ΐΙΊœΒ»γΆΦΥυ ΨΘ§œ¬Ν–ΥΒΖ®¥μΈσΒΡ «Θ® Θ©

AΘ°–ΓΟς÷–ΆΨ–ίœΔ”ΟΝΥ20Ζ÷÷”
BΘ°–ΓΟς–ίœΔ«Α≈ά…ΫΒΡΤΫΨυΥΌΕ»ΈΣΟΩΖ÷÷”70ΟΉ
CΘ°–ΓΟς‘Ύ…œ ωΙΐ≥Χ÷–ΥυΉΏΒΡ¬Ζ≥ΧΈΣ6600ΟΉ
DΘ°–ΓΟς–ίœΔ«Α≈ά…ΫΒΡΤΫΨυΥΌΕ»¥σ”Ύ–ίœΔΚσ≈ά…ΫΒΡΤΫΨυΥΌΕ»
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
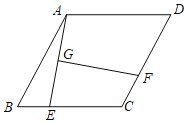
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΡ±Ώ–ΈABCDΈΣΝβ–ΈΘ§ΓœD=60ΓψΘ§AB=4Θ§EΈΣ±ΏBC…œΒΡΕ·ΒψΘ§Ν§Ϋ”AEΘ§ΉςAEΒΡ¥Ι÷±ΤΫΖ÷œΏGFΫΜ÷±œΏCD”ΎFΒψΘ§¥ΙΉψΈΣΒψGΘ§‘ρœΏΕΈGFΒΡΉν–Γ÷ΒΈΣ____________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§÷±œΏyΘΫ![]() x+b”κ÷±œΏyΘΫ
x+b”κ÷±œΏyΘΫ![]() xΫΜ”ΎΒψAΘ®mΘ§1Θ©Θ°”κy÷αΫΜ”ΎΒψB
xΫΜ”ΎΒψAΘ®mΘ§1Θ©Θ°”κy÷αΫΜ”ΎΒψB
Θ®1Θ©«σmΒΡ÷ΒΚΆΒψBΒΡΉχ±ξΘΜ
Θ®2Θ©»τΒψC‘Ύy÷α…œΘ§«“ΓςABCΒΡΟφΜΐ «1Θ§«κ÷±Ϋ”–¥≥ωΒψCΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ ΐ÷α…œ”–»ΐΒψAΓΔBΓΔCΘ§»τ”ΟAB±μ ΨAΓΔBΝΫΒψΒΡΨύάκΘ§AC±μ ΨAΓΔCΝΫΒψΒΡΨύάκΘ§«“ABΘΫ![]() ACΘ§ΒψAΓΔΒψCΕ‘”ΠΒΡ ΐ «Ζ÷±π «aΓΔcΘ§«“|a+40|+|c©¹20|ΘΫ0Θ°
ACΘ§ΒψAΓΔΒψCΕ‘”ΠΒΡ ΐ «Ζ÷±π «aΓΔcΘ§«“|a+40|+|c©¹20|ΘΫ0Θ°
![]()
Θ®1Θ©«σBCΒΡ≥ΛΘ°
Θ®2Θ©»τΒψPΓΔQΖ÷±π¥”AΓΔCΝΫΒψΆ§ ±≥ωΖΔœρΉσ‘ΥΕ·Θ§ΥΌΕ»Ζ÷±πΈΣ2ΗωΒΞΈΜ≥ΛΕ»ΟΩΟκΓΔ5ΗωΒΞΈΜ≥ΛΕ»ΟΩΟκΘ§‘ρ‘ΥΕ·ΝΥΕύ…ΌΟκ ±Θ§QΒΫBΒΡΨύάκ”κPΒΫBΒΡΨύάκœύΒ»ΘΩ
Θ®3Θ©»τΒψPΓΔQ»‘»Μ“‘Θ®2Θ©÷–ΒΡΥΌΕ»Ζ÷±π¥”AΓΔCΝΫΒψΆ§ ±≥ωΖΔœρΉσ‘ΥΕ·Θ§2ΟκΚσΘ§Ε·ΒψR¥”AΒψ≥ωΖΔœρ”“‘ΥΕ·Θ§ΒψRΒΡΥΌΕ»ΈΣ1ΗωΒΞΈΜ≥ΛΕ»ΟΩΟκΘ§ΒψMΈΣœΏΕΈPRΒΡ÷–ΒψΘ§ΒψNΈΣœΏΕΈRQΒΡ÷–ΒψΘ§ΒψR‘ΥΕ·ΝΥΕύ…ΌΟκ ±«ΓΚΟ¬ζΉψMN+AQΘΫ31ΘΜ≤Δ«σ≥ω¥Υ ±RΒψΥυΕ‘”ΠΒΡ ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœACB=90ΓψΘ§ΒψDΘ§EΖ÷±π «±ΏBCΘ§AB…œΒΡ÷–ΒψΘ§Ν§Ϋ”DE≤Δ―”≥Λ÷ΝΒψFΘ§ ΙEF=2DFΘ§Ν§Ϋ”CEΓΔAFΘ°
Θ®1Θ©÷ΛΟςΘΚAF=CEΘΜ
Θ®2Θ©Β±ΓœB=30Γψ ±Θ§ ‘≈–ΕœΥΡ±Ώ–ΈACEFΒΡ–ΈΉ¥≤ΔΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com