
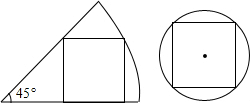
 一张圆心角为45°的扇形纸板和圆形纸板按如图方式剪得一个正方形,边长都为2,则扇形纸板和圆形纸板的面积比是( )
一张圆心角为45°的扇形纸板和圆形纸板按如图方式剪得一个正方形,边长都为2,则扇形纸板和圆形纸板的面积比是( )| A. | 5:4 | B. | 5:2 | C. | $\sqrt{5}$:2 | D. | $\sqrt{5}$:$\sqrt{2}$ |
分析 分别求出扇形和圆的半径,再根据扇形和圆的面积公式求出面积,最后求出比值即可.
解答 解:如图1,连接OD,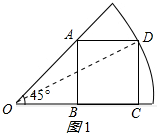
∵四边形ABCD是正方形,
∴∠DCB=∠ABO=90°,AB=BC=CD=2,
∵∠AOB=45°,
∴OB=AB=2,
由勾股定理得:OD=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∴扇形的面积是$\frac{45π×(2\sqrt{5})^{2}}{360}$=$\frac{5}{2}$π;
如图2,连接MB、MC,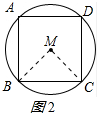
∵四边形ABCD是⊙M的内接四边形,四边形ABCD是正方形,
∴∠BMC=90°,MB=MC,
∴∠MCB=∠MBC=45°,
∵BC=2,
∴MC=MB=$\sqrt{2}$,
∴⊙M的面积是π×($\sqrt{2}$)2=2π,
∴扇形和圆形纸板的面积比是$\frac{5}{2}$π÷(2π)=$\frac{5}{4}$.
故选:A.
点评 本题考查了正方形性质、圆内接四边形性质、扇形的面积公式的应用;解此题的关键是求出扇形和圆的面积,题目比较好,难度适中.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | -[-x]=[x] | B. | [2x]=2[x] | C. | [x+y]≤[x]+[y] | D. | [x-y]≤[x]-[y] |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
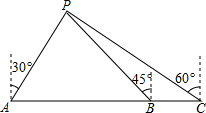 天宜号船向正东方航行(如图),船在A处时测得灯塔在P北偏东30°方向,前进到B处时测得灯塔P恰好在西北方向,又航行半小时到达C处,此时测得灯塔P在北偏西60°方向,若船速为每小时20海里,求A、C两点间的距离.
天宜号船向正东方航行(如图),船在A处时测得灯塔在P北偏东30°方向,前进到B处时测得灯塔P恰好在西北方向,又航行半小时到达C处,此时测得灯塔P在北偏西60°方向,若船速为每小时20海里,求A、C两点间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com