
【题目】如图,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.
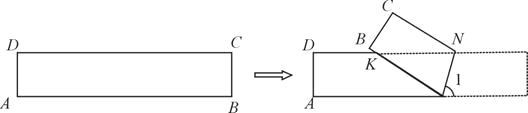

(1)若∠1=70°,求∠MKN的度数.
(2)△MNK的面积能否小于![]() ?若能,求出此时∠1的度数;若不能,试说明理由.
?若能,求出此时∠1的度数;若不能,试说明理由.
(3)如何折叠能够使△MNK的面积最大?请你利用备用图探究可能出现的情况,求出最大值.
【答案】(1)、40°;(2)、不能,理由见解析;(3)、1.3
【解析】试题分析:根据折叠图形的性质求出角的度数;过M点作ME⊥DN,垂足为点E,则ME=AD=1,然后得出三角形的面积大于等于![]() 即可得出答案;分两种情况进行讨论计算,得出最大值.
即可得出答案;分两种情况进行讨论计算,得出最大值.
试题解析:(1)40°
(2)不能. 过M点作ME⊥DN,垂足为点E,则ME=AD=1, 由(1)知∠KNM=∠KMN.∴MK=NK.
又MK≥ME, ∴NK≥1. ∴![]() .
.
∴△MNK的面积最小值为![]() ,不可能小于
,不可能小于![]() .
.
(3)分两种情况:
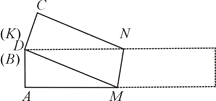
情况一:将矩形纸片对折,使点B与点D重合,此时点K也与点D重合.
设MK=MD=x,则AM=5-x,由勾股定理,得
![]() ,
,
解得, ![]() .即
.即![]() .
.
∴![]() .
.
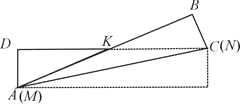 情况二:将矩形纸片沿对角线AC对折,此时折痕为AC.
情况二:将矩形纸片沿对角线AC对折,此时折痕为AC.
设MK="AK=" CK=x,则DK=5-x,同理可得
即![]() .
.
∴![]() .
.
∴△MNK的面积最大值为1.3.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,且
的直径,且![]() ,点
,点![]() 为
为![]() 的延长线上一点,过点
的延长线上一点,过点![]() 作
作![]() 的切线
的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() .
.
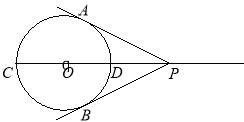
(1)、连接![]() ,若
,若![]() ,试证明
,试证明![]() 是等腰三角形;
是等腰三角形;
(2)、填空:①当![]() =
= ![]() 时,四边形
时,四边形![]() 是菱形;②当
是菱形;②当![]() =
= ![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题的逆命题是真命题的是( )
A. 如果a>0,b>0,则a+b>0
B. 直角都相等
C. 两直线平行,同位角相等
D. 若a=6,则|a|=|6|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
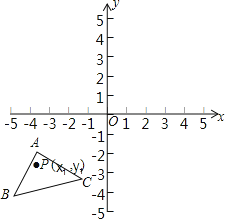
(1)请在图中作出△A′B′C′;
(2)写出点A′、B′、C′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当![]() 很大时,摸到白球的频率将会接近 .(精确到0.1)
很大时,摸到白球的频率将会接近 .(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)= .
(3)试估算盒子里黑、白两种颜色的球各有多少只?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com