
【题目】已知△ABC与△CEF均为等腰直角三角形,∠ABC=∠CFE=90°,连接AE,点G是AE中点,连接BG和GF.
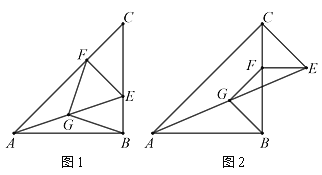
(1)如图1,当△CEF中E、F落在BC、AC边上时,探究FG与BG的关系;
(2)如图2,当△CEF中F落在BC边上时,探究FG与BG的关系.
【答案】(1) FG=BG,FG⊥BG;证明见详解;(2)FG=BG,FG⊥BG;证明见详解;
【解析】
(1)由∠AFE=∠ABE=90°,点G是AE中点,则![]() ,
,![]() ,则得到FG=BG,∠FGE=2∠FAG,∠BGE=2∠BAG,由∠FAG+∠BAG=45°,即可得到∠BGF=90°;
,则得到FG=BG,∠FGE=2∠FAG,∠BGE=2∠BAG,由∠FAG+∠BAG=45°,即可得到∠BGF=90°;
(2)过点E作ED⊥AB,交AB延长线于点D,连接DG,CG,根据题意,找出相应的条件证明△GFE≌△GBD(SAS),得到FG=BG,与(1)证法一样,证明∠CGD=90°,通过等量代换即可得到∠FGB=90°.
解:(1)FG=BG,FG⊥BG;如图1,
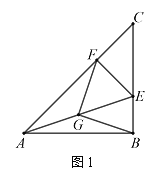
∵∠ABC=∠CFE=90°,
∴△ABE和△AFE是直角三角形,
∵点G是AE的中点,
∴![]() ,
,![]() ,
,
∴![]() .,∠GAF=∠GFA,∠GAB=∠GBA,
.,∠GAF=∠GFA,∠GAB=∠GBA,
∴∠FGE=2∠FAG,∠BGE=2∠BAG,
∵∠BAC=∠FAG+∠BAG=45°
∴∠BGF=∠FGE+∠BGE=2(∠FAG+∠BAG)=90°,
即FG⊥BG;
(2)![]() ,
,![]() ;
;
过点E作ED⊥AB,交AB延长线于点D,连接DG,CG,
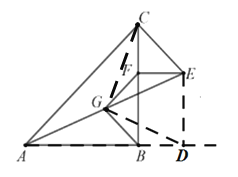
∵△ABC与△CEF均为等腰直角三角形,ED⊥AB,
∴∠FBD=∠BFE=∠EDB=90°,
∴四边形BFED是矩形,
∴BD=EF,
在直角三角形ADE和直角三角形ACE中,G是AE中点,
∴DG=GE=AG=CG=![]() ,
,
∴∠GED=∠GDE,
∴∠FEG=∠BDG,
∴△GFE≌△GBD(SAS),
∴GF=GB,CF=BD,
∵DG=AG=CG,
∴△CGF≌△DGB,∠CAG=∠ACG,∠DAG=∠ADG,
∴∠CGF=∠DGB,
∵∠CAG+∠DAG=45°,
∠CGE+∠DGE=2(∠CAG+∠DAG)=90°,
即∠CGD=90°,
∴∠CGD-∠CGF+∠DGB=∠FGB=90°,
即FG⊥BG.


科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民开始选购家用净水器.一商家抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元?(注:毛利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),B点坐标为(5,0)点C(0,5),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MAB的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区将原来400平方米的正方形场地改建成300平方米的长方形场地,且长和宽之比为3∶2.如果把原来正方形场地的铁栅栏围墙利用起来围成新场地的长方形围墙,那么这些铁栅栏是否够用?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足为A,B,连接AB,下列结论中不一定成立的是( )

A.PA=PBB.PO平分∠APBC.OA=OBD.AB平分OP
查看答案和解析>>
科目:初中数学 来源: 题型:
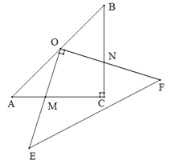
【题目】如图,在Rt△ACB中,AC=BC=8,O为AB的中点,以O为直角顶点作等腰直角三角形OEF,与边AC,BC相交于点M,N.有下列结论:①AM=CN;②CM+CN=8;③![]() ;④当M是AC的中点时,OM=ON.其中正确结论的序号是______.
;④当M是AC的中点时,OM=ON.其中正确结论的序号是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解八年级学生对![]() (科学)、
(科学)、![]() (技术)、
(技术)、![]() (工程)、
(工程)、![]() (艺术)、
(艺术)、![]() (数学)中哪一个领域最感兴趣的情况,该校对八年级学生进行了抽样调查,根据调查结果绘制成如下的条形图和扇形图,请根据图中提供的信息,解答下列问题:
(数学)中哪一个领域最感兴趣的情况,该校对八年级学生进行了抽样调查,根据调查结果绘制成如下的条形图和扇形图,请根据图中提供的信息,解答下列问题:

(1)这次抽样调查共调查了多少名学生?
(2)补全条形统计图;
(3)求扇形统计图中![]() (数学)所对应的圆心角度数;
(数学)所对应的圆心角度数;
(4)若该校八年级学生共有400人,请根据样本数据估计该校八年级学生中对![]() (科学)最感兴趣的学生大约有多少人?
(科学)最感兴趣的学生大约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com