练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为(-1，0)，B点坐标为（5,0）点C(0，5)，M为它的顶点.

    (1)求抛物线的解析式；

    (2)求△MAB的面积。

    【答案】（1） y=-x2+4x+5 (2) 27

    【解析】

    试题（1）将已知的三点坐标代入抛物线中，即可求得抛物线的解析式；

    （2）求出二次函数的顶点坐标，根据三角形面积计算公式求出答案．

    试题解析：∵二次函数y=ax2+bx+c（a≠0）的图象经过（-1，0）、（0，5）和（0，5），

    ∴，

    ∴，

    ∴抛物线的解析式为y=-x2+4x+5；

    （2）∵B点坐标为（5，0），

    ∴AB=5-（-1）=6，

    ∵y=-x2+4x+5，

    ∴y=-（x-2）2+9，

    ∴抛物线图象的顶点坐标为（2，9），

    ∴S△AMB=×6×9=27．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在四边形ABCD中，，对角线AC平分．

    如图1，若，，探究AD、AB与对角线AC三者之间的数量关系，写出结论，不必证明．

    如图2若将中的条件“”去掉，中的结论是否还成立？并证明你的结论；

    如图3，若，试探究AD、AB与对角线AC三者之间的数量关系，写出结论，不必证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在矩形ABCD中，AB=3，AD=4，动点P从点B出发，以每秒1个单位的速度，沿BA向点A移动；同时点Q从点C出发，以每秒2个单位的速度，沿CB向点B移动，连接QP，QD，PD．若两个点同时运动的时间为x秒（0<x≤2），解答下列问题：

    （1）当x为何值时，PQ⊥DQ；

    （2）设△QPD的面积为S，用含x的函数关系式表示S；当x为何值时，S有最小值？并求出最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠ACB＝90°，AC＝BC，BE⊥CE于点E，AD⊥CE于点D，下面四个结论：①∠ABE＝∠BAD；②△CEB≌△ADC；③AB＝CE；④AD－BE＝DE.其中正确的结论是____.(把所有正确结论的序号都写在横线上)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,已知△ABC中,∠B=90°，AB=8，CB=6，P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.

    (1)当t=2秒时,求PQ的长;

    (2)求出发时间为几秒时,△PQB是等腰三角形?

    (3)若Q沿B→C→A方向运动,则当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若一个数能表示成某个整数的平方的形式，则称这个数为完全平方数，完全平方数是非负数．例如：0＝02，1＝12，4＝22，9＝32，16＝42，25＝52，36＝62，121＝112…．

    （1）若28+210+2n是完全平方数，求n的值．

    （2）若一个正整数，它加上61是一个完全平方数，当减去11是另一个完全平方数，写出所有符合的正整数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：和同一平面内的点．

    （1）如图1，若点在边上过点作交于点，作交于点．根据题意，请在图1中补全图形，并直接写出与的数量关系；

    （2）如图2，若点在的延长线上，且，．请判断与的位置关系并说明理由；

    （3）如图3，点是外部的一点，过点作交直线于点，作交直线于点，请直接写出与的数量关系，并图3中补全图形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

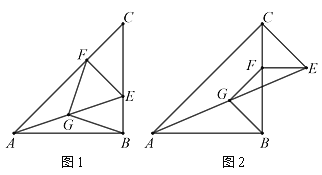
    【题目】已知△ABC与△CEF均为等腰直角三角形，∠ABC＝∠CFE＝90°，连接AE，点G是AE中点，连接BG和GF．

    （1）如图1，当△CEF中E、F落在BC、AC边上时，探究FG与BG的关系；

    （2）如图2，当△CEF中F落在BC边上时，探究FG与BG的关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知∠A+∠E+∠F+∠C=540°．

    （1）试判断直线AB与CD的位置关系，并说明理由；

    （2）如图2，∠PAB=3∠PAQ，∠PCD=3∠PCQ，试判断∠APC与∠AQC的数量关系，并说明理由．

    查看答案和解析>>

    同步练习册答案