练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在矩形ABCD中，AB=3，AD=4，动点P从点B出发，以每秒1个单位的速度，沿BA向点A移动；同时点Q从点C出发，以每秒2个单位的速度，沿CB向点B移动，连接QP，QD，PD．若两个点同时运动的时间为x秒（0<x≤2），解答下列问题：

    （1）当x为何值时，PQ⊥DQ；

    （2）设△QPD的面积为S，用含x的函数关系式表示S；当x为何值时，S有最小值？并求出最小值．

    【答案】（1）1.25（2）当x=1.5时，S有最小值为3.75

    【解析】分析：（1）可知 先判定 得到 即 解出x的值即得答案.

    用矩形的面积减去三个直角三角形的面积即可表示出，根据二次函数的性质求解即可.

    详解：（1）当时，

    又∵四边形ABCD是矩形，

    ∴

    ∴

    ∴，

    ∴

    ∴即

    得

    （2）

    ∴当时，S有最小值为3.75.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知在图一中，将等边绕BC边中点D顺时针旋转至，直线AG与直线CF交于点求证．小明同学的思路是这样的：通过证明∽得到，从而得到，继续推理就可以使问题得到解决．

    请根据小明的思路，求证：；

    爱动脑筋的小明把问题做了进一步思考，他想：如果把题目的“等边”改成“等腰直角，其中，”，如图二，中的结论还成立吗？如果成立，求此时线段BM的最大值．

    小明继续大胆设问：如图三，在中，，，将这样的按照题目中的方式旋转，请直接写出AG与CF的位置关系以及线段BM的变化范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在课外活动时间，甲、乙、丙做“互相踢毽子”游戏，毽子从一人传给另一人就记为一次踢毽．

    若从甲开始，经过三次踢毽后，毽子踢到乙处的概率是多少？请说明理由；

    若经过三次踢毽后，毽子踢到乙处的可能性最小，则应从______开始踢．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为提高饮水质量，越来越多的居民开始选购家用净水器．一商家抓住商机，从厂家购进了A、B两种型号家用净水器共160台，A型号家用净水器进价是150元/台，B型号家用净水器进价是350元/台，购进两种型号的家用净水器共用去36000元．

    （1）求A、B两种型号家用净水器各购进了多少台；

    （2）为使每台B型号家用净水器的毛利润是A型号的2倍，且保证售完这160台家用净水器的毛利润不低于11000元，求每台A型号家用净水器的售价至少是多少元？（注：毛利润=售价﹣进价）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，O为坐标原点，四边形OABC为长方形，A(10，0)，C(0，4)，D是OA的中点，点P在线段BC上运动．

    （1）B的坐标为_________；

    （2）当∠POD＝30°时，求CP的长；

    （3）当△DPO是腰长为5的等腰三角形时，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】设(a，b)是一次函数y＝(k-2)x+m与反比例函数的图象的交点，且a、b是关于x的一元二次方程的两个不相等的实数根，其中k为非负整数，m、n为常数．

    （1）求k的值；

    （2）求一次函数与反比例函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解某校落实新课改精神的情况，现以该校九年级二班的同学参加课外活动的情况为样本，对其参加“球类”、“绘画类”、“舞蹈类”、“音乐类”、“棋类”活动的情况进行调查统计，并绘制了如图所示的统计图．

    （1）参加音乐类活动的学生人数为 人，参加球类活动的人数的百分比为 ；

    （2）请把图2（条形统计图）补充完整；

    （3）该校学生共600人，则参加棋类活动的人数约为 ；

    （4）该班参加舞蹈类活动的4位同学中，有1位男生（用E表示）和3位女生（分别用F，G，H表示），先准备从中选取两名同学组成舞伴，请用列表或画树状图的方法求恰好选中一男一女的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为(-1，0)，B点坐标为（5,0）点C(0，5)，M为它的顶点.

    (1)求抛物线的解析式；

    (2)求△MAB的面积。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

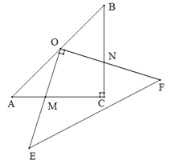
    【题目】如图，在Rt△ACB中，AC=BC=8，O为AB的中点，以O为直角顶点作等腰直角三角形OEF,与边AC，BC相交于点M，N.有下列结论：①AM=CN；②CM+CN=8；③；④当M是AC的中点时，OM=ON.其中正确结论的序号是______.

    查看答案和解析>>

    同步练习册答案