
【题目】某学校为了解该校七年级学生的身高情况,抽样调查了部分同学,将所得数据处理后,制成扇形统计图和频数分布直方图(部分)如下(每组只含最低值不含最高值,身高单位:cm,测量时精确到1cm):
(1)请根据所提供的信息计算身高在160~165cm范围内的学生人数,并补全频数分布直方图;
(2)样本的中位数在统计图的哪个范围内?
(3)如果上述样本的平均数为157cm,方差为0.8;该校八年级学生身高的平均数为159cm,方差为0.6,那么(填“七年级”或“八年级”)学生的身高比较整齐.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
A种产品 | B种产品 | |
成本(万元∕件) | 3 | 5 |
利润(万元∕件) | 1 | 2 |
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)条件下,哪种方案获利最大?并求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图题:
(1)如图,将△ABC绕点O顺时针旋转180°后得到△A1B1C1 . 请你画出旋转后的△A1B1C1; 
(2)请你画出下面“蒙古包”的左视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OD垂直于弦AB,垂足为点C,连接AO并延长交⊙O于点E,连接BE,CE.若AB=8,CD=2,则△BCE的面积为( ) 
A.12
B.15
C.16
D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE. 
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强与小刚都住在安康小区,在同一所学校读书,某天早上,小强7:30从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留2分钟,校车行驶途中始终保持匀速,当天早上,小刚7:39从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早1分钟到学校站点,他们乘坐的车辆从安康小区站出发所行使路程y(千米)与行驶时间x(分钟)之间的函数图象如图所示. 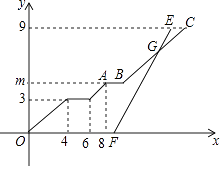
(1)求点A的纵坐标m的值;
(2)小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车?并求此时他们距学校站点的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N. 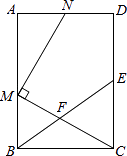
(1)当F为BE中点时,求证:AM=CE;
(2)若 ![]() =2,求
=2,求 ![]() 的值;
的值;
(3)若 ![]() =n,当n为何值时,MN∥BE?
=n,当n为何值时,MN∥BE?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com