
【题目】若关于x的分式方程 ![]() 无解,则m的值为( )
无解,则m的值为( )
A.-1.5
B.1
C.-1.5或2
D.-0.5或-1.5
【答案】D
【解析】解:方程两边都乘以x(x-3)得:(2m+x)x-x(x-3)=2(x-3),
即(2m+1)x=-6,
分两种情况考虑:
①∵当2m+1=0时,此方程无解,
∴此时m=-0.5,
②∵关于x的分式方程 ![]() 无解,
无解,
∴x=0或x-3=0,
即x=0,x=3,
当x=0时,代入(2m+1)x=-6得:0=-6,
解得:此方程无解;
当x=3时,代入(2m+1)x=-6得:(2m+1)×3=-6,
解得:m=-1.5,
∴m的值是-0.5或-1.5,
故选D.
【考点精析】通过灵活运用去分母法和分式方程的增根,掌握先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊;使方程的分母为0的解称为原方程的增根即可以解答此题.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探究:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.
猜想结论:(要求用文字语言叙述)
写出证明过程(先画出图形,写出已知、求证).
(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+c(a≠0)的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).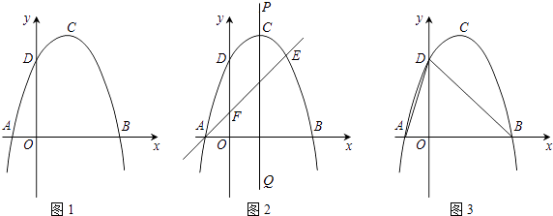
(1)求抛物线的解析式;
(2)如图2,过点A的直线与抛物线交于点 E,交y轴于点F,其中点E的横坐标为2,若直线PQ为抛物线的对称轴,点G为直线 PQ上的一动点,则x轴上是否存在一点H,使D、G,H、F四点所围成的四边形周长最小?若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由;
(3)如图3,在抛物线上是否存在一点T,过点T作x轴的垂线,垂足为点M,过点M作MN∥BD,交线段AD于点N,连接MD,使△DNM∽△BMD?若存在,求出点T的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某品牌电风扇销售量的情况,对某商场5月份该品牌甲、乙、丙三种型号的电风扇销售量进行统计,绘制如下两个统计图(均不完整).请你结合图中的信息,解答下列问题: 
(1)该商场5月份售出这种品牌的电风扇共多少台?
(2)若该商场计划订购这三种型号的电风扇共2000台,根据5月份销售量的情况,求该商场应订购丙种型号电风扇多少台比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解该校七年级学生的身高情况,抽样调查了部分同学,将所得数据处理后,制成扇形统计图和频数分布直方图(部分)如下(每组只含最低值不含最高值,身高单位:cm,测量时精确到1cm):
(1)请根据所提供的信息计算身高在160~165cm范围内的学生人数,并补全频数分布直方图;
(2)样本的中位数在统计图的哪个范围内?
(3)如果上述样本的平均数为157cm,方差为0.8;该校八年级学生身高的平均数为159cm,方差为0.6,那么(填“七年级”或“八年级”)学生的身高比较整齐.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中: ①∠ABC=∠ADC;
②AC与BD相互平分;
③AC,BD分别平分四边形ABCD的两组对角;
④四边形ABCD的面积S= ![]() ACBD.
ACBD.
正确的是(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABOC的顶点O在坐标原点,顶点B,C分别在x,y轴的正半轴上,顶点A在反比例函数y= ![]() (k为常数,k>0,x>0)的图象上,将矩形ABOC绕点A按逆时针反向旋转90°得到矩形AB′O′C′,若点O的对应点O′恰好落在此反比例函数图象上,则
(k为常数,k>0,x>0)的图象上,将矩形ABOC绕点A按逆时针反向旋转90°得到矩形AB′O′C′,若点O的对应点O′恰好落在此反比例函数图象上,则 ![]() 的值是 .
的值是 . 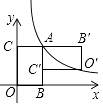
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com