
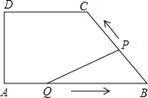
【题目】如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题:
(1)当t为何值时,P,Q两点同时停止运动?
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值.
【答案】(1)、5;(2)、![]() ;(3)、t=
;(3)、t=![]() s,
s,![]() s或t=4s
s或t=4s
【解析】试题分析:(1)、通过比较线段AB,BC的大小,找出较短的线段,根据速度公式可以直接求得;(2)、由已知条件,把△PQB的边QB用含t的代数式表示出来,三角形的高可由相似三角形的性质也用含t的代数式表示出来,代入三角形的面积公式可得到一个二次函数,即可求出S的最值;(3)、根据等腰三角形的性质和余弦公式列出等式求解,即可求的结论.
试题解析:(1)、作CE⊥AB于E, ∵DC∥AB,DA⊥AB, ∴四边形AECD是矩形,
∴AE=CD=5,CE=AD=4, ∴BE=3, ∴BC=5, ∴BC<AB,
∴P到C时,P、Q同时停止运动, ∴t=![]() (秒), 即t=5秒时,P,Q两点同时停止运动.
(秒), 即t=5秒时,P,Q两点同时停止运动.
(2)、由题意知,AQ=BP=t, ∴QB=8﹣t, 作PF⊥QB于F,则△BPF~△BCE,
∴![]() ,即
,即![]() , ∴BF=
, ∴BF=![]() ,
,![]()
∴S=![]() QBPF=
QBPF=![]() ×
×![]() (8﹣t)=﹣
(8﹣t)=﹣![]() (t﹣4)2+
(t﹣4)2+![]() (0<t≤5),
(0<t≤5),
∵﹣![]() <0, ∴S有最大值,当t=4时,S的最大值是
<0, ∴S有最大值,当t=4时,S的最大值是![]() ;
;
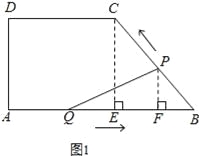
(3)、∵cos∠B=![]() , ①当PQ=PB时(如图2所示),则BG=
, ①当PQ=PB时(如图2所示),则BG=![]() BQ,
BQ,![]() =
=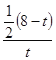 =
=![]() ,解得t=
,解得t=![]() s,
s,
②当PQ=BQ时(如图3/span>所示),则BG=![]() PB,
PB,![]() =
=![]() =
=![]() ,解得t=
,解得t=![]() s,
s,
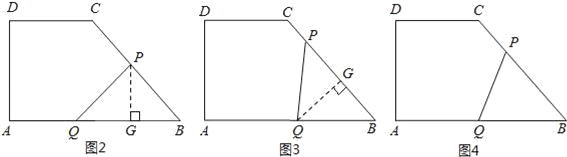
③当BP=BQ时(如图4所示),则8﹣t=t, 解得:t=4.
综上所述:当t=![]() s,
s,![]() s或t=4s时,△PQB为等腰三角形.
s或t=4s时,△PQB为等腰三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() x﹣4分别与x轴、y轴交于点A和点B,点C、D分别是线段OA、AB的中点,点P为OB上一动点,当PC+PD取最小值时点P的坐标是( )
x﹣4分别与x轴、y轴交于点A和点B,点C、D分别是线段OA、AB的中点,点P为OB上一动点,当PC+PD取最小值时点P的坐标是( )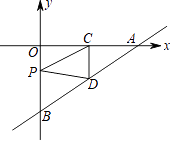
A.(0,﹣1)
B.(0,﹣2)
C.(0,﹣3)
D.(0,﹣4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为 ;抛物线的解析式为 .
(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图2中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在13×13的网格图中,已知△ABC和点M(1,2).
(1)以点M为位似中心,画出△ABC的位似图形△A′B′C′,其中△A′B′C′与△ABC的位似比为2;
(2)写出△A′B′C′的各顶点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设置了两种促销方式.一种方式是:让顾客通过转转盘获得购物券.规定顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准100元、50元、20元的相应区域,那么顾客就可以分别获得100元、50元、20元购物券,凭购物券可以在该商场继续购物;如果指针对准其他区域,那么就不能获得购物券.另一种方式是:不转转盘,顾客每购买100元的商品,可直接获得10元购物券.据统计,一天中共有1 000人次选择了转转盘的方式,其中指针落在100元、50元、20元的次数分别为50次、100次、200次.
(1)指针落在不获奖区域的概率约是多少?
(2)通过计算说明选择哪种方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣3,﹣3),B(﹣2,﹣1),C(﹣1,﹣2)是直角坐标平面上三点.
(1)请画出△ABC关于原点O对称的△A1B1C1;
(2)请写出点B关于y轴对称的点B2的坐标,若将点B2向上平移h个单位,使其落在△A1B1C1内部,指出h的取值范围.
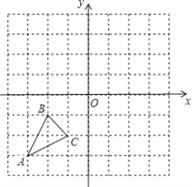
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次学科测验,学生得分均为整数,满分10分,成绩达到6分以上为合格.成绩达到9分为优秀.这次测验中甲乙两组学生成绩分布的条形统计图如下: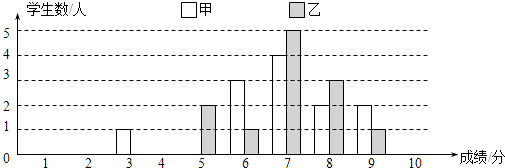
(1)请补充完成下面的成绩统计分析表:
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
甲组 | 6.9 | 2.4 | 91.7% | 16.7% | |
乙组 | 1.3 | 83.3% | 8.3% |
(2)甲组学生说他们的合格率、优秀率均高于乙组,所以他们的成绩好于乙组.但乙组学生不同意甲组学生的说法,认为他们组的成绩要高于甲组.请你给出三条支持乙组学生观点的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com