
| 甲 | 乙 | |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |
|
|
|


科目:初中数学 来源: 题型:
 如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.
如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,点G为对角线交点,顶点A在x轴上,顶点C的坐标为(0,6),∠COB=30°,以OC上一点P为圆心,以
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,点G为对角线交点,顶点A在x轴上,顶点C的坐标为(0,6),∠COB=30°,以OC上一点P为圆心,以| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
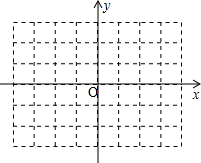 (1)在给出的直角坐标系中,画出两条一次函数图象,使得它们都满足;当自变量-1≤x≤1时,其函数值的取值范围为-2≤y≤3;
(1)在给出的直角坐标系中,画出两条一次函数图象,使得它们都满足;当自变量-1≤x≤1时,其函数值的取值范围为-2≤y≤3;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com