
����Ŀ�����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O������ǡ�DOC����������DOC����ʱ�뷽����ת�õ���D��OC����0������ת�ǣ�90��������AC����BD����AC����BD���ཻ�ڵ�M��
��1�����ı���ABCD�Ǿ���ʱ����ͼ1�������AC����BD����������ϵ�Լ���AMB�����Ĵ�С��ϵ����֤����IJ��룻
��2�����ı���ABCD��ƽ���ı���ʱ����ͼ2����֪AC��kBD��������ʱAC����BD����������ϵ�Լ���AMB�����Ĵ�С��ϵ����֤����IJ��룻
��3�����ı���ABCD�ǵ�������ʱ����ͼ3��AD��BC����ʱ��1��AC����BD����������ϵ�Ƿ��������AMB�����Ĵ�С��ϵ�Ƿ����������֤����ֱ��д�����ۣ�
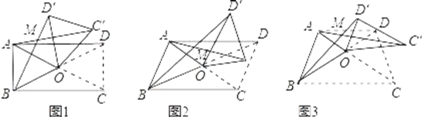
���𰸡���1��BD����AC������AMB����������������2��AC����kBD������AMB����������������3��AC����BD����������AMB����������
��������
��1��ͨ��֤����BOD���ա�AOC���õ�BD����AC������OBD������OAC���������������ڽǺͶ��������AMB����AOB����COD������
��2�����ݣ�1����˼·֤����BOD���ס�AOC�����õ�AC����kBD������BD����OA�ཻ�ڵ�N��������֤�á�BNO����ANM���ٸ����������ڽǺ������AMB������
��3�������õ������ε�����OA=OD,OB=OC,��������ת֤��![]() ,�ɴ�֤����
,�ɴ�֤����![]() �ա�
�ա�![]() ���õ�BD����AC������Ӧ�ǵĵ�����ϵ���ɴ�֤�á�AMB������������
���õ�BD����AC������Ӧ�ǵĵ�����ϵ���ɴ�֤�á�AMB������������
�⣺��1��AC����BD������AMB������
֤�����ھ���ABCD�У�AC��BD��OA��OC��![]() AC��OB��OD��
AC��OB��OD��![]() BD��
BD��
��OA��OC��OB��OD��
�֡�OD��OD����OC��OC����
��OB��OD����OA��OC����
�ߡ�D��OD����C��OC��
��180������D��OD��180������C��OC��
���BOD������AOC����
���BOD���ա�AOC����
��BD����AC����
���OBD������OAC����
��BD����OA�ཻ�ڵ�N��
���BNO����ANM��
��180������OAC������ANM��180������OBD������BNO��
����AMB����AOB����COD������
����������BD����AC������AMB������
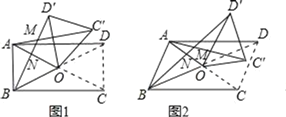
��2��AC����kBD������AMB������
֤��������ƽ���ı���ABCD�У�OB��OD��OA��OC��
�֡�OD��OD����OC��OC����
��OC����OA��OD����OB��
�ߡ�D��OD����C��OC��
��180������D��OD��180������C��OC��
���BOD������AOC����
���BOD���ס�AOC����
��BD����AC����OB��OA��BD��AC��
��AC��kBD��
��AC����kBD����
�ߡ�BOD���ס�AOC����
��BD����OA�ཻ�ڵ�N��
���BNO����ANM��
��180������OAC������ANM��180������OBD������BNO������AMB����AOB������
����������AC����kBD������AMB������
��3�����ڵ�������ABCD�У�OA=OD,OB=OC,
����ת�ã� ![]() ,
,
��![]() ,
,
��![]() ,
,
���![]() �ա�
�ա�![]() ,
,
��AC����BD��, ![]() ,
,
��BD����OA�ཻ�ڵ�N��
�ߡ�ANB=![]() +��AMB=
+��AMB=![]() ,
,![]() ,
,
��![]() ,
,
��AC����BD����������AMB������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�ǽ����żƻ������ij��й㳡��һ�鳤���οյ�����һ�����Ϊ1200m2��ͣ��������ͣ�����������µĿյ�����ͬ������ͨ������֪�����οյصij�Ϊ50m����Ϊ40m��

��1����ͨ���Ŀ��ȣ�
��2��ij��˾ϣ����80��Ԫ�ijа����������㳡�Ĺ��̣��ǽ�������Ϊ���̫����Ҫ���ۣ�ͨ������Э�̣�������51.2��Ԫ���һ�£������ν��۵İٷ�����ͬ����ÿ�ν��۵İٷ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y��kx��1(k��0)�뷴��������y��![]() (m��0)��ͼ���й�����A(1��2)��ֱ��l��x���ڵ�N(3��0)����һ�κ����ͷ�����������ͼ��ֱ��ཻ�ڵ�B��C������AC.
(m��0)��ͼ���й�����A(1��2)��ֱ��l��x���ڵ�N(3��0)����һ�κ����ͷ�����������ͼ��ֱ��ཻ�ڵ�B��C������AC.
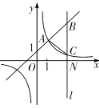
(1)��k��m��ֵ��
(2)���B�����ꣻ
(3)����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB��3��BC��4����E��AB����һ�㣬��AE��2����F�DZ�BC�ϵ�����һ�㣬�ѡ�BEF��EF���ۣ���B�Ķ�Ӧ��ΪG������AG��CG�����ı���AGCD���������СֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺����֪�����ı��ε�һ���Խ��߰�����ı��ηֳ������������Σ�������������������ƣ���ȫ�ȣ������ǾͰ������Խ��߽�������ı��ε������ƶԽ�������
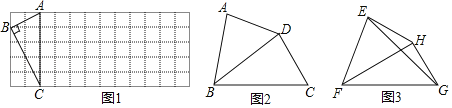
��1����ͼ1����֪Rt��ABC�������������У�����ֻ���̶ȵ�ֱ�����������ҵ�һ��D��ʹ�ı���ABCD����ACΪ�����ƶԽ��������ı��Σ�������ͼ�ۼ�����
��2����ͼ2�����ı���ABCD�У���ABC��70������ADC��145�����Խ���BDƽ�֡�ABC����֤��BD���ı���ABCD�������ƶԽ�������
��3����ͼ3����֪FH���ı���EFGH�������ƶԽ���������EFH����HFG��30��������EG������EFG�����Ϊ2![]() ����FH�ij���
����FH�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��12�·ݣ�����ӭ�����Ҽ��������и��飬Ϊ���˽�ѧ�����������е��˽������ѧУ�����ȡ�˲���ѧ�������ʾ����飬��������������A�dz��˽�![]() �˽�
�˽�![]() �˽����
�˽����![]() ���˽�������ֱ�ͳ�ƣ�����������������ͳ��ͼ(������
���˽�������ֱ�ͳ�ƣ�����������������ͳ��ͼ(������![]() �����ͼ����Ϣ������������⣺
�����ͼ����Ϣ������������⣺
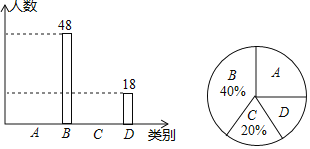
![]() �˴ι�������______��ѧ����
�˴ι�������______��ѧ����
![]() ����ͳ��ͼ��D���ڵ����ε�Բ�Ľ�Ϊ______��
����ͳ��ͼ��D���ڵ����ε�Բ�Ľ�Ϊ______��
![]() ������ͳ��ͼ����������
������ͳ��ͼ����������
![]() ����У����800��ѧ����������ƶ��������е��˽����Ϊ���dz��˽�����ѧ����������
����У����800��ѧ����������ƶ��������е��˽����Ϊ���dz��˽�����ѧ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
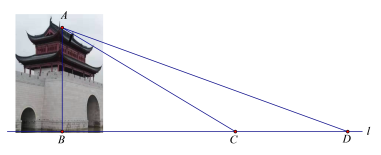
����Ŀ��ˮ����λ�ڵ��ֺӺ���ۺ�����ڣ��ǻ���ˮϵ�����ֺ��ε���������Ҫ�ı�־�Ծ��ۣ��ڿ���ʵ����У�ijУ���꼶��ѧ��ȤС�����������ˮ���ŵĸߣ����ǵIJ����������£���ͼ������D����õ�A������Ϊ20��������ˮ���ŵķ���ǰ��13����C������õ�A������Ϊ31������D��C��B��һֱ���ϣ������ˮ����AB�ĸߣ�����ȷ��0.1�ף�
���ο����ݣ�sin20���0.34��cos20���0.94��tan20���0.36��sin31���0.52��cos31���0.86��tan31���0.60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�ACƽ����DAB����ADC=��ACB=90�㣬EΪAB���е㣬
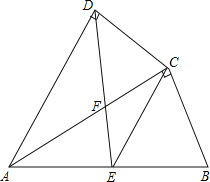
��1����֤��AC2=ABAD��
��2����֤��CE��AD��
��3����AD=4��AB=6���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y����2x2+bx+c��ͼ���㣨0��6���ͣ�1��8����
��1����������κ����Ľ���ʽ��
��2���ٵ�x��ʲô��Χ��ʱ��y��x�����������
�ڵ�x��ʲô��Χ��ʱ��y��0��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com