
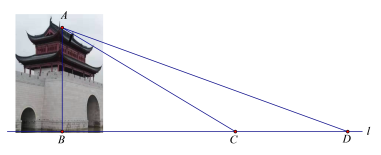
【题目】水城门位于淀浦河和漕港河三叉口,是环城水系公园淀浦河梦蝶岛区域重要的标志性景观.在课外实践活动中,某校九年级数学兴趣小组决定测量该水城门的高.他们的操作方法如下:如图,先在D处测得点A的仰角为20°,再往水城门的方向前进13米至C处,测得点A的仰角为31°(点D、C、B在一直线上),求该水城门AB的高.(精确到0.1米)
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() ,已知
,已知![]() ,抛物线的对称轴交
,抛物线的对称轴交![]() 轴于点
轴于点![]() .
.
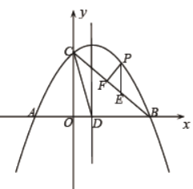
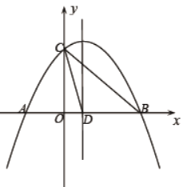
备用图
(1)求该抛物线的解析式;
(2)连接![]() ,能否在抛物线上找到一点
,能否在抛物线上找到一点![]() ,使得
,使得![]() ,若有求
,若有求![]() 点的坐标,若没有说明理由;
点的坐标,若没有说明理由;
(3)若点![]() 为
为![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,当
,当![]() 的周长最大时,求点
的周长最大时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
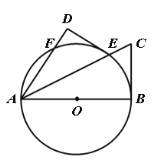
【题目】如图,已知AB是⊙O的直径,F是⊙O上一点,∠BAF的平分线交⊙O于点E,交⊙O的切线BC于点C,过点E作ED⊥AF,交AF的延长线于点D.
(1)求证:DE是⊙O的切线;
(2)若DE=3,CE=2,
①求![]() 值;
值;
②若点G 为AE上一点,求OG+![]() EG最小值.
EG最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
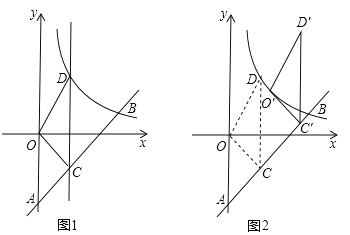
【题目】(2016江苏省镇江市) (2016镇江)如图1,一次函数y=kx﹣3(k≠0)的图象与y轴交于点A,与反比例函数![]() (x>0)的图象交于点B(4,b).
(x>0)的图象交于点B(4,b).
(1)b= ;k= ;
(2)点C是线段AB上的动点(于点A、B不重合),过点C且平行于y轴的直线l交这个反比例函数的图象于点D,求△OCD面积的最大值;
(3)将(2)中面积取得最大值的△OCD沿射线AB方向平移一定的距离,得到△O′C′D′,若点O的对应点O′落在该反比例函数图象上(如图2),则点D′的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
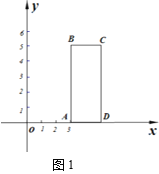
【题目】如图1,在矩形ABCD中,AB=5,AD=2,把它放在x轴的正半轴上,AD与x轴重合且点A坐标为(3,0).
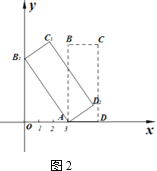
(1)若以点A为旋转中心,将矩形ABCD逆时针旋转,使点B落到y轴上的点B1处,得到矩形AB1C1D1,如图2,求点B1,C1,D1的坐标.
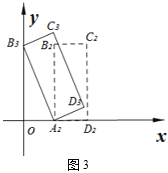
(2)若将矩形ABCD向左平移一段距离后得到矩形A2B2C2D2,如图3,再将它以A2为旋转中心逆时针旋转,使点B2落到y轴上的点B3处.此时点C3恰好落在点A2的正上方得到矩形A2B3C3D3,求平移的距离并写出C3的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]() ,当
,当![]() 时,函数有最大值
时,函数有最大值![]() .
.
(1)求此二次函数图象与坐标轴的交点;
(2)将函数![]() 图象
图象![]() 轴下方部分沿
轴下方部分沿![]() 轴向上翻折,得到的新图象,若点
轴向上翻折,得到的新图象,若点![]() 是翻折得到的抛物线弧部分上任意一点,若关于
是翻折得到的抛物线弧部分上任意一点,若关于![]() 的一元二次方程
的一元二次方程![]() 恒有实数根时,求实数
恒有实数根时,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某便利店的咖啡单价为10元/杯,为了吸引顾客,该店共推出了三种会员卡,如下表:
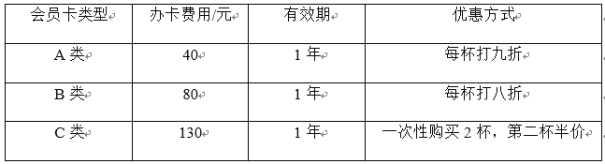
例如,购买A类会员卡,1年内购买50次咖啡,每次购买2杯,则消费40+2×50×(0.9×10)=940元. 若小玲1年内在该便利店购买咖啡的次数介于75~85次之间,且每次购买2杯,则最省钱的方式为
A.购买A类会员卡B.购买B类会员卡C.购买C类会员卡D.不购买会员卡
查看答案和解析>>
科目:初中数学 来源: 题型:
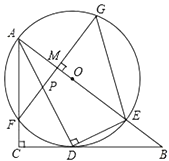
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是角平分线,
是角平分线,![]() 交
交![]() 于
于![]() ,
,![]() 的外接圆
的外接圆![]() 与边
与边![]() 相交于点
相交于点![]() ,过
,过![]() 作
作![]() 的垂线交
的垂线交![]() 于
于![]() ,交
,交![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的半径;
的半径;
(3)在(2)的条件下,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com