
【题目】已知:二次函数![]() ,当
,当![]() 时,函数有最大值
时,函数有最大值![]() .
.
(1)求此二次函数图象与坐标轴的交点;
(2)将函数![]() 图象
图象![]() 轴下方部分沿
轴下方部分沿![]() 轴向上翻折,得到的新图象,若点
轴向上翻折,得到的新图象,若点![]() 是翻折得到的抛物线弧部分上任意一点,若关于
是翻折得到的抛物线弧部分上任意一点,若关于![]() 的一元二次方程
的一元二次方程![]() 恒有实数根时,求实数
恒有实数根时,求实数![]() 的最大值.
的最大值.
【答案】(1)抛物线与![]() 轴交于(0,-3),与
轴交于(0,-3),与![]() 轴交于(-1,0),(3,0);(2)实数
轴交于(-1,0),(3,0);(2)实数![]() 的最大值为3
的最大值为3
【解析】
(1)求出对称轴![]() ,结合
,结合![]() ,可知当
,可知当![]() 时,
时,![]() 随
随![]() 增大而增大,所以
增大而增大,所以![]() 时,
时,![]() ,把
,把![]() ,
,![]() 代入解析式求出
代入解析式求出![]() 的值,然后解方程
的值,然后解方程![]() 即可;
即可;
(2)折叠部分对应的解析式:![]() ,根据
,根据![]() 求出
求出![]() 的取值范围,即
的取值范围,即![]() ,再结合
,再结合![]() ,即可求得实数
,即可求得实数![]() 的最大值.
的最大值.
(1)抛物线![]() 的对称轴为:
的对称轴为:![]() .
.
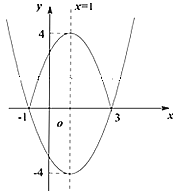
∴![]() ,抛物线开口向上,大致图象如图所示.
,抛物线开口向上,大致图象如图所示.
当![]() 时,
时,![]() 随
随![]() 增大而增大;
增大而增大;
∵当![]() 时,函数有最大值
时,函数有最大值![]() ,
,
∴当![]() 时,
时,![]() ,
,
∴![]() ,
,
解得:![]() .
.
∴![]()
当![]() ,
,![]() ,
,
![]() ,x2-2x-3=0,
,x2-2x-3=0,
解得:![]() 或
或![]() ,
,
∴抛物线与![]() 轴交于
轴交于![]() ,抛物线与
,抛物线与![]() 轴交于
轴交于![]() ,
,![]() .
.
(2)∵关于![]() 的一元二次方程
的一元二次方程![]() 恒有实数根,
恒有实数根,
∴![]() ,即
,即![]() 恒成立,
恒成立,
∴![]() 恒成立.
恒成立.
∵(1)中的抛物线解析式为y=x2-2x-3,
∴函数的最小值为![]() =-4,
=-4,
∵点![]() 是(1)中抛物线沿x轴翻折得到的抛物线弧部分上任意一点,
是(1)中抛物线沿x轴翻折得到的抛物线弧部分上任意一点,
∴![]() ,
,
∴![]() (k取
(k取![]() 值的下限),
值的下限),
∴实数![]() 的最大值为3.
的最大值为3.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某区招聘新教师即将进入面试环节,除了从外区抽调部分评委之外,还打算从本区教学专家库中每门学科再随机抽取2人,共同组成评委团队担任面试工作.已知该区初中数学学科专家库中共有6名候选人:杨老师(女)、王老师(男),陈老师(女)、周老师(男)、王老师(女)、李老师(女).由于李老师(女)有直系亲属参加面试需回避,所以本区的2名初中数学学科评委只能在其余5人中随机产生.请用画树状图法或列表法等方式求出“所抽取的2名评委恰好是都是女教师”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
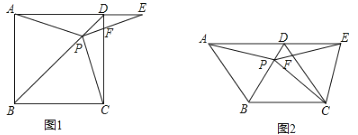
【题目】如图,在正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 上的一点,点
上的一点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)证明:![]() ;
;
(2)如图,把正方形![]() 改为菱形
改为菱形![]() ,其它条件不变,当
,其它条件不变,当![]() 时,连接
时,连接![]() ,试探究线段
,试探究线段![]() 与线段
与线段![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
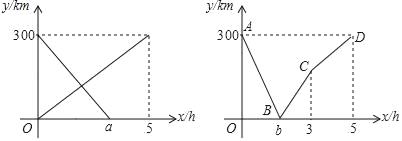
【题目】一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,设快车离乙地的距离为y1(km),慢车离乙地的距离为y2(km),慢车行驶时间为x(h),两车之间的距离为s(km).y1,y2与x的函数关系图象如图1所示,s与x的函数关系图象如图2所示.则下列判断:①图1中a=3;②当x=![]() h时,两车相遇;③当x=
h时,两车相遇;③当x=![]() 时,两车相距60km;④图2中C点坐标为(3,180);⑤当x=
时,两车相距60km;④图2中C点坐标为(3,180);⑤当x=![]() h或
h或![]() h时,两车相距200km.其中正确的有_____(请写出所有正确判断的序号)
h时,两车相距200km.其中正确的有_____(请写出所有正确判断的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P,Q是方格纸中的两格点,请按要求画出以PQ为对角线的格点四边形.
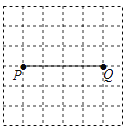
(1)在图1中画出一个面积最小的¨PAQB;
(2)在图2中画出一个四边形PCQD,使其是轴对称图形而不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.注:图1,图2在答题纸上.
查看答案和解析>>
科目:初中数学 来源: 题型:
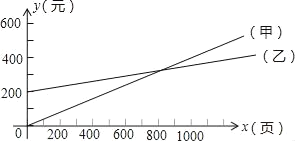
【题目】学校有一批复印任务,原来由甲复印社承接,按每100页40元计费.现乙复印社表示:若学校先按月付给一定数额的承包费,则可按每100页15元收费.两复印社每月收费情况如图所示.
(1)乙复印社的每月承包费是 元;
(2)当每月复印 页时两复印社实际收费相同,费用是 元;
(3)甲的复印社的函数式是 ,如果每月复印页数在1200页左右那么应选择 复印社合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
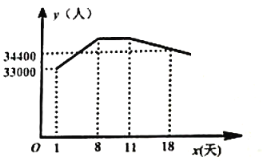
【题目】某市植物园于2019年3月-5月举办花展,按照往年的规律推算,自4月下旬起游客量每天增加![]() 人,游客量预计将在5月1日达到高峰,并持续到5月4日,随后游客量每天有所减少.已知4月24日为第一天起,每天的游客量
人,游客量预计将在5月1日达到高峰,并持续到5月4日,随后游客量每天有所减少.已知4月24日为第一天起,每天的游客量![]() (人)与时间
(人)与时间![]() (天)的函数图像如图所示,结合图像提供的信息,解答下列问题:
(天)的函数图像如图所示,结合图像提供的信息,解答下列问题:
![]() 已知该植物园门票
已知该植物园门票![]() 元/张,若每位游客在园内每天平均消费
元/张,若每位游客在园内每天平均消费![]() 元,试求5月1日-5月4日,所有游客消费总额为多少元?
元,试求5月1日-5月4日,所有游客消费总额为多少元?
![]() 当
当![]() 时,求
时,求![]() 关于
关于![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
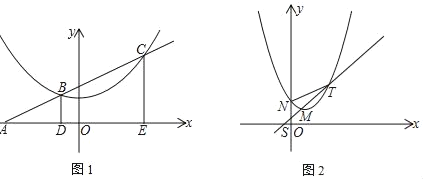
【题目】如图,已知直线:y=kx+3k与x轴交于A点,与抛物线y=![]() +1交于点B、C两点
+1交于点B、C两点
(1)若k=1,求点B、C(点B在点C的左边)的坐标;
(2)过B、C分别作x轴的垂线,垂足分别为点D、E,求ADAE的值;
(3)将抛物线y=![]() +1沿直线y=mx+1(m>1)向右平移t个单位,直线y=mx+1交y轴于S,交新抛物线于MT,N是新抛物线与y轴的交点,试探究t为何值时,NT∥x轴?
+1沿直线y=mx+1(m>1)向右平移t个单位,直线y=mx+1交y轴于S,交新抛物线于MT,N是新抛物线与y轴的交点,试探究t为何值时,NT∥x轴?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标;
(3)抛物线上是否存在一点Q(Q与B不重合),使△CDQ的面积等于△BCD的面积?若存在,直接写出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com