
【题目】某区招聘新教师即将进入面试环节,除了从外区抽调部分评委之外,还打算从本区教学专家库中每门学科再随机抽取2人,共同组成评委团队担任面试工作.已知该区初中数学学科专家库中共有6名候选人:杨老师(女)、王老师(男),陈老师(女)、周老师(男)、王老师(女)、李老师(女).由于李老师(女)有直系亲属参加面试需回避,所以本区的2名初中数学学科评委只能在其余5人中随机产生.请用画树状图法或列表法等方式求出“所抽取的2名评委恰好是都是女教师”的概率.
 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=x2﹣4的图象与x轴交于点A、B(点A位于点B的左侧),C为顶点.一次函数y=mx+2的图象经过点A,与y轴交于点D.
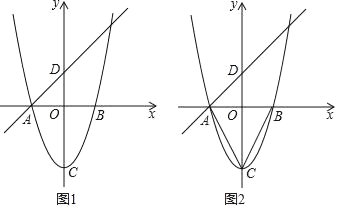
(1)求直线AD的函数表达式;
(2)平移该抛物线得到一条新抛物线,设新抛物线的顶点为C′.若新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD,且当1≤x≤3时,新抛物线对应的函数值有最小值为﹣1,求新抛物线对应的函数表达式;
(3)如图,连接AC、BC,在坐标平面内,直接写出使得△ACD与△EBC相似(其中点A与点E是对应点)的点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表显示了同学们用计算机模拟随机投针实验的某次实验的结果.
投针次数n | 1000 | 2000 | 3000 | 4000 | 5000 | 10000 | 20000 |
针与直线相交的次数m | 454 | 970 | 1430 | 1912 | 2386 | 4769 | 9548 |
针与直线相交的频率p=
| 0.454 | 0.485 | 0.4767 | 0.478 | 0.4772 | 0.4769 | 0.4774 |
下面有三个推断:
①投掷1000次时,针与直线相交的次数是454,针与直线相交的概率是0.454;
②随着实验次数的增加,针与直线相交的频率总在0.477附近,显示出一定的稳定性,可以估计针与直线相交的概率是0.477;
③若再次用计算机模拟此实验,则当投掷次数为10000时,针与直线相交的频率一定是0.4769.
其中合理的推断的序号是:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的平分线分别交AB、BD于点M、N,若AD=4,则线段AM的长为( )
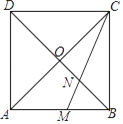
A. 2B. 2![]() C. 4﹣
C. 4﹣![]() D. 8﹣4
D. 8﹣4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,如果一个矩形的宽与长之比为![]() ,那么这个矩形就称为黄金矩形.如图,已知A、B两点都在反比例函数y=
,那么这个矩形就称为黄金矩形.如图,已知A、B两点都在反比例函数y=![]() (k>0)位于第一象限内的图像上,过A、B两点分别作坐标轴的垂线,垂足分别为C、D和E、F,设AC与BF交于点G,已知四边形OCAD和CEBG都是正方形.设FG、OC的中点分别为P、Q,连接PQ.给出以下结论:①四边形ADFG为黄金矩形;②四边形OCGF为黄金矩形;③四边形OQPF为黄金矩形.以上结论中,正确的是( )
(k>0)位于第一象限内的图像上,过A、B两点分别作坐标轴的垂线,垂足分别为C、D和E、F,设AC与BF交于点G,已知四边形OCAD和CEBG都是正方形.设FG、OC的中点分别为P、Q,连接PQ.给出以下结论:①四边形ADFG为黄金矩形;②四边形OCGF为黄金矩形;③四边形OQPF为黄金矩形.以上结论中,正确的是( )
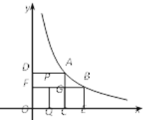
A. ①B. ②C. ②③D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点P是BC边上一动点,连结AP,AP的垂直平分线交BD于点G,交 AP于点E,在P点由B点到C点的运动过程中,∠APG的大小变化情况是( )
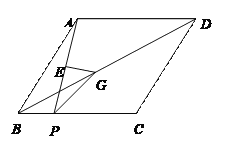
A. 变大 B. 先变大后变小 C. 先变小后变大 D. 不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△PMN中,∠P=90°,PM=PN,MN=6cm,矩形ABCD中AB=2cm,BC=10cm,点C和点M重合,点B、C(M)、N在同一直线上,令Rt△PMN不动,矩形ABCD沿MN所在直线以每秒1cm的速度向右移动,至点C与点N重合为止,设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y,则y与x的大致图象是( )
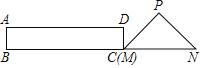
A. 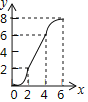 B.
B. 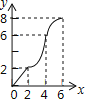 C.
C. 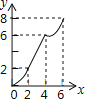 D.
D. 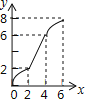
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+3的图象经过A(﹣1,0)、C(3,0)、并且与y轴相交于点B,点P是直线BC上方的抛物线上的一动点,PQ∥y轴交直线BC于点Q.
(1)求此二次函数的表达式;
(2)求线段PQ的最大值;
(3)在抛物线的对称轴上,是否存在点M,使△MAB为等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
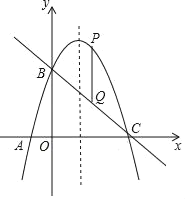
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]() ,当
,当![]() 时,函数有最大值
时,函数有最大值![]() .
.
(1)求此二次函数图象与坐标轴的交点;
(2)将函数![]() 图象
图象![]() 轴下方部分沿
轴下方部分沿![]() 轴向上翻折,得到的新图象,若点
轴向上翻折,得到的新图象,若点![]() 是翻折得到的抛物线弧部分上任意一点,若关于
是翻折得到的抛物线弧部分上任意一点,若关于![]() 的一元二次方程
的一元二次方程![]() 恒有实数根时,求实数
恒有实数根时,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com