
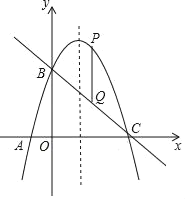
【题目】已知二次函数y=ax2+bx+3的图象经过A(﹣1,0)、C(3,0)、并且与y轴相交于点B,点P是直线BC上方的抛物线上的一动点,PQ∥y轴交直线BC于点Q.
(1)求此二次函数的表达式;
(2)求线段PQ的最大值;
(3)在抛物线的对称轴上,是否存在点M,使△MAB为等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3;(2)![]() ;(3)M1(1,1),M2(1,
;(3)M1(1,1),M2(1,![]() ),M3(1,﹣
),M3(1,﹣![]() ),M4(1,0).
),M4(1,0).
【解析】
(1)利用待定系数法确定函数关系式即可;(2)设P(﹣m,﹣m2+2m+3),Q(m,﹣m+3).利用两点间的距离公式得到PQ=﹣m2+3m,再利用配方法求得最值即可;(3)分①MA=MB, ②MA=AB,③AB=MB三种情况求点M的坐标即可.
解:(1)∵二次函数y=ax2+bx+3的图象经过A(﹣1,0),C(3,0).
∴![]()
解得![]() .
.
∴此二次函数表达式为y=﹣x2+2x+3.
(2)∵设直线BC为y=kx+b,因其经过B(0,3),C(3,0),
∴![]() .
.
解得k=﹣1,b=3
∴直线BC的表达式为y=﹣x+3.
设P(﹣m,﹣m2+2m+3),Q(m,﹣m+3)
PQ=﹣m2+2m+3﹣(﹣m+3)
=﹣m2+3m
=﹣(m﹣![]() )2+
)2+![]() .
.
PQ的最大值为![]() .
.
(3)存在,理由如下:
∵二次函数y=﹣x2+2x+3的对称轴为x=﹣![]() =1,OA=1,OB=3,
=1,OA=1,OB=3,
在Rt△ABO中由勾股定理可得AB=![]() ,AB2=10.
,AB2=10.
设M(1,a),则MA2=22+a2,MB2=12+(a﹣3)2.
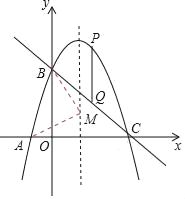
分三种情况讨论:
①MA=MB,22+a2=12+(a﹣3)2,得a=1,
∴M1(1,1);
②MA=AB,22+a2=10,得a=±![]() ,
,
∴M2(1,![]() ),M3(1,﹣
),M3(1,﹣![]() );
);
③AB=MB,12+(a﹣3)2=10,得a=0或a=6,
∴M4(1,0),M5(1,6).
∵M5、A、B三点共线,
∴M5(1,6)舍去.
∴M的坐标为:M1(1,1),M2(1,![]() ),M3(1,﹣
),M3(1,﹣![]() ),M4(1,0).
),M4(1,0).


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
【题目】某种乐器有10个孔,依次记作第1孔,第2孔,……,第10孔,演奏时,第n孔与其音色的动听指数D之间满足关系式![]() ,该乐器的最低动听指数为4k+106,求常数k的取值范围。
,该乐器的最低动听指数为4k+106,求常数k的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区招聘新教师即将进入面试环节,除了从外区抽调部分评委之外,还打算从本区教学专家库中每门学科再随机抽取2人,共同组成评委团队担任面试工作.已知该区初中数学学科专家库中共有6名候选人:杨老师(女)、王老师(男),陈老师(女)、周老师(男)、王老师(女)、李老师(女).由于李老师(女)有直系亲属参加面试需回避,所以本区的2名初中数学学科评委只能在其余5人中随机产生.请用画树状图法或列表法等方式求出“所抽取的2名评委恰好是都是女教师”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以80海里/小时的速度继续航行多少小时即可到达?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
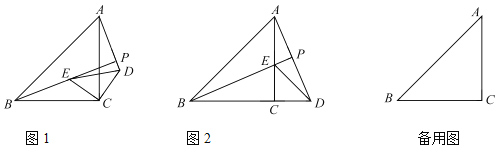
【题目】如图1,![]() 和
和![]() 均为等腰三角形,且
均为等腰三角形,且![]() ,连接
,连接![]() ,
,![]() ,两条线段所在的直线交于点
,两条线段所在的直线交于点![]() .
.
(1)线段![]() 与
与![]() 有何数量关系和位置关系,请说明理由.
有何数量关系和位置关系,请说明理由.
(2)若已知![]() ,
,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,
顺时针旋转,
①如图2,当点![]() 恰好落在
恰好落在![]() 的延长线上时,求
的延长线上时,求![]() 的长;
的长;
②在旋转一周的过程中,设![]() 的面积为
的面积为![]() ,求
,求![]() 的最值.
的最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
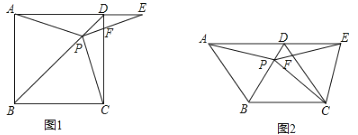
【题目】如图,在正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 上的一点,点
上的一点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)证明:![]() ;
;
(2)如图,把正方形![]() 改为菱形
改为菱形![]() ,其它条件不变,当
,其它条件不变,当![]() 时,连接
时,连接![]() ,试探究线段
,试探究线段![]() 与线段
与线段![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
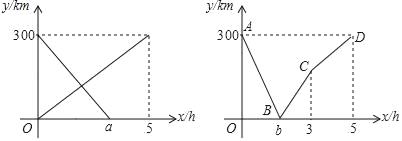
【题目】一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,设快车离乙地的距离为y1(km),慢车离乙地的距离为y2(km),慢车行驶时间为x(h),两车之间的距离为s(km).y1,y2与x的函数关系图象如图1所示,s与x的函数关系图象如图2所示.则下列判断:①图1中a=3;②当x=![]() h时,两车相遇;③当x=
h时,两车相遇;③当x=![]() 时,两车相距60km;④图2中C点坐标为(3,180);⑤当x=
时,两车相距60km;④图2中C点坐标为(3,180);⑤当x=![]() h或
h或![]() h时,两车相距200km.其中正确的有_____(请写出所有正确判断的序号)
h时,两车相距200km.其中正确的有_____(请写出所有正确判断的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
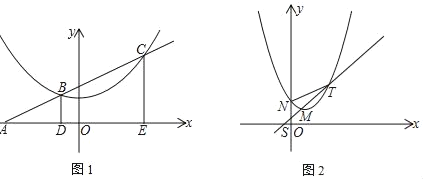
【题目】如图,已知直线:y=kx+3k与x轴交于A点,与抛物线y=![]() +1交于点B、C两点
+1交于点B、C两点
(1)若k=1,求点B、C(点B在点C的左边)的坐标;
(2)过B、C分别作x轴的垂线,垂足分别为点D、E,求ADAE的值;
(3)将抛物线y=![]() +1沿直线y=mx+1(m>1)向右平移t个单位,直线y=mx+1交y轴于S,交新抛物线于MT,N是新抛物线与y轴的交点,试探究t为何值时,NT∥x轴?
+1沿直线y=mx+1(m>1)向右平移t个单位,直线y=mx+1交y轴于S,交新抛物线于MT,N是新抛物线与y轴的交点,试探究t为何值时,NT∥x轴?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com