
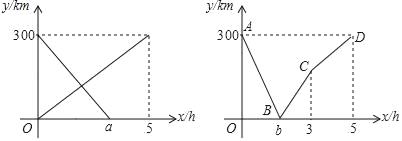
����Ŀ��һ���쳵�Ӽؿ����ҵأ�һ���������ҵؿ����أ�����ͬʱ��������쳵���ҵصľ���Ϊy1��km�����������ҵصľ���Ϊy2��km����������ʻʱ��Ϊx��h��������֮��ľ���Ϊs��km����y1��y2��x�ĺ�����ϵͼ����ͼ1��ʾ��s��x�ĺ�����ϵͼ����ͼ2��ʾ���������жϣ���ͼ1��a��3���ڵ�x��![]() hʱ�������������۵�x��
hʱ�������������۵�x��![]() ʱ���������60km����ͼ2��C������Ϊ��3��180�����ݵ�x��
ʱ���������60km����ͼ2��C������Ϊ��3��180�����ݵ�x��![]() h��
h��![]() hʱ���������200km��������ȷ����_____����д��������ȷ�жϵ���ţ�
hʱ���������200km��������ȷ����_____����д��������ȷ�жϵ���ţ�
���𰸡��٢ڢܣ�
��������
����S��x֮��ĺ�����ϵʽ���Եõ���λ��C��ʱ������֮��ľ������ӱ仺����ʱ�쳵��վ����ʱa=3���ʢ���ȷ������������֪y1=y2���з������ɵ�x��ֵΪ![]() ���ʢ���ȷ��������������ǣ�����ǰ���������������60km��x��
���ʢ���ȷ��������������ǣ�����ǰ���������������60km��x��![]() ������ǰ��ʱ�䣬�ʢ���ȷ����ȷ��b��ֵ�����ݺ�����ͼ����Եõ�C�ĵ�����꣬�ʢ���ȷ������������ǰ����������������������ۣ��������x��ֵ����x=
������ǰ��ʱ�䣬�ʢ���ȷ����ȷ��b��ֵ�����ݺ�����ͼ����Եõ�C�ĵ�����꣬�ʢ���ȷ������������ǰ����������������������ۣ��������x��ֵ����x=![]() hʱ�������⣬�ʢݲ���ȷ��
hʱ�������⣬�ʢݲ���ȷ��
�⣺����S��x֮��ĺ�����ͼ���֪����λ��C��ʱ������֮��ľ������ӱ仺��
���ɴ˿��Եõ�a��3���ʢ���ȷ��
��y1��kx+b������0��300������3��0�����룬
�ã�![]() ����ã�
����ã�![]() ��
��
��y1����100x+300��
��y2��mx��
���㣨5��300�����룬�ã�5m��300��
��ã�m��60��
���������ҵصľ���y2����ʽΪ��y2��60x��
�൱y1��y2ʱ������������
�ɵã���100x+300��60x��
��ã�x��![]() h���ʢ���ȷ��
h���ʢ���ȷ��
������������ǣ�����ǰ�������60km��
��100x+300��60x��60����ã�x=![]() h��
h��
�������������60km��
60x������100x+300����60����ã�x=![]() h��
h��
�൱x��![]() h��
h��![]() hʱ���������60km���ʢ۲���ȷ��
hʱ���������60km���ʢ۲���ȷ��
�쳵ÿСʱ��ʻ![]() ��100ǧ�ף�����ÿСʱ��ʻ60ǧ�ף�����֮��ľ���Ϊ300ǧ�ף�
��100ǧ�ף�����ÿСʱ��ʻ60ǧ�ף�����֮��ľ���Ϊ300ǧ�ף�
��b��300����100+60����![]() ��
��
�ɺ�����ͼ����Եõ�C�ĵ�ĺ�����Ϊ3�����쳵�����ҵأ���ʱ�������ߵ�·��Ϊ3��60��180ǧ�ף�
��C������Ϊ��3��180�����ʢ���ȷ��
������������ǣ�����ǰ�������200km��
��100x+300��60x��200����ã�x=![]() h��
h��
�������������60km��
60x������100x+300����200����ã�x=![]() h��
h��
��![]() >3��
>3��
�൱x=![]() h�������⣬��ȥ��
h�������⣬��ȥ��
�൱x��![]() hʱ���������200km���ʢݲ���ȷ��
hʱ���������200km���ʢݲ���ȷ��
�ʴ�Ϊ���٢ڢܣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
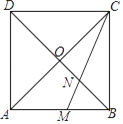
����Ŀ����ͼ��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����ACB��ƽ���߷ֱ�AB��BD�ڵ�M��N����AD��4�����߶�AM�ij�Ϊ��������
A. 2B. 2![]() C. 4��
C. 4��![]() D. 8��4
D. 8��4![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
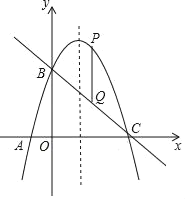
����Ŀ����֪���κ���y��ax2+bx+3��ͼ��A����1��0����C��3��0����������y���ཻ�ڵ�B����P��ֱ��BC�Ϸ����������ϵ�һ���㣬PQ��y�ύֱ��BC�ڵ�Q��
��1����˶��κ����ı���ʽ��
��2�����߶�PQ�����ֵ��
��3���������ߵĶԳ����ϣ��Ƿ���ڵ�M��ʹ��MABΪ���������Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
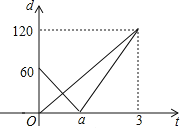
����Ŀ��С�����Ƶ�����ֱ���˶�ң�س�ģ�ͼס�������ͬʱ�ֱ��![]() ��
��![]() ��������ֱ�߹��ͬʱ����
��������ֱ�߹��ͬʱ����![]() ������֪�ҵ��ٶ��Ǽ��ٶȵ�1.5�����ס�����ң�س���
������֪�ҵ��ٶ��Ǽ��ٶȵ�1.5�����ס�����ң�س���![]() ���ľ���
���ľ���![]() ��
��![]() ���ף���ʱ��
���ף���ʱ��![]() �����ӣ��ĺ�����ϵ��ͼ��ʾ�������н����У���
�����ӣ��ĺ�����ϵ��ͼ��ʾ�������н����У���![]() �ľ���Ϊ120�ף����ҵ��ٶ�Ϊ60��/�֣���
�ľ���Ϊ120�ף����ҵ��ٶ�Ϊ60��/�֣���![]() ��ֵΪ
��ֵΪ![]() �������ס�����ң�س��ľ��벻����10��ʱ�������źŲ������������ţ��������źŲ������������ŵ�
�������ס�����ң�س��ľ��벻����10��ʱ�������źŲ������������ţ��������źŲ������������ŵ�![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]() ��������ȷ���У� ����
��������ȷ���У� ����
A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У���A��B��C������ֱ�Ϊ����1��3��������4��1��������2��1��������ABC��һȷ������ƽ�Ƶõ���A1B1C1����B�Ķ�Ӧ��B1�������ǣ�1��2�������A1��C1������ֱ��� ��������

A. A1��4��4����C1��3��2�� B. A1��3��3����C1��2��1��
C. A1��4��3����C1��2��3�� D. A1��3��4����C1��2��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��ͼ����ͼ��ʾ���������н��ۣ���2a+b��0��
��b��a��c������-1��m��n��1����m+n��![]() ����3|a|+|c|��2|b|��������ȷ�Ľ��۸����ǣ� ��
����3|a|+|c|��2|b|��������ȷ�Ľ��۸����ǣ� ��
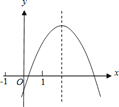
A. �٢ۢ� B. �٢� C. �٢� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����κ���![]() ����
����![]() ʱ�����������ֵ
ʱ�����������ֵ![]() .
.
(1)��˶��κ���ͼ����������Ľ��㣻
(2)������![]() ͼ��
ͼ��![]() ���·�������
���·�������![]() �����Ϸ��ۣ��õ�����ͼ������
�����Ϸ��ۣ��õ�����ͼ������![]() �Ƿ��۵õ�������������������һ�㣬������
�Ƿ��۵õ�������������������һ�㣬������![]() ��һԪ���η���
��һԪ���η���![]() ����ʵ����ʱ����ʵ��
����ʵ����ʱ����ʵ��![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BDΪ��ABC���Բ��O��ֱ�����ҡ�BAE=��C��
��1����֤��AE���O�����ڵ�A��
��2����AE��BC��BC=2![]() ��AC=2
��AC=2![]() ����AD�ij���
����AD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ��
��![]() ��
��![]() ���е�.��
���е�.��![]() ��
��![]() ������
������![]() ���ӳ�
���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �������н�����ȷ���У� ����.
�������н�����ȷ���У� ����.
��1��![]() ��2��
��2��![]()
��3��![]() �������18 ��4��
�������18 ��4��![]()

A. 4B. 3C. 2D. 1
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com