
【题目】二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①2a+b>0;
②b>a>c;③若-1<m<n<1,则m+n<![]() ;④3|a|+|c|<2|b|.其中正确的结论个数是( )
;④3|a|+|c|<2|b|.其中正确的结论个数是( )
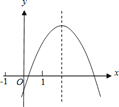
A. ①③④ B. ①③ C. ①④ D. ②③④
【答案】A
【解析】∵抛物线开口向下,∴a<0,∴2a<0,对称轴x=-![]() >1,-b<2a,∴2a+b>0,故①正确;
>1,-b<2a,∴2a+b>0,故①正确;
∵-b<2a,∴b>-2a>0>a,
令抛物线解析式为y=-![]() x 2 +bx-
x 2 +bx-![]() ,此时a=c,欲使抛物线与x轴交点的横坐标分别为
,此时a=c,欲使抛物线与x轴交点的横坐标分别为![]() 和2,则
和2,则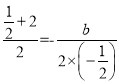 ,解得:b=
,解得:b=![]() ,
,
∴抛物线y=-![]() x 2 +
x 2 +![]() x-
x-![]() ,符合“开口向下,与x轴的一个交点的横坐标在0与1之间,
,符合“开口向下,与x轴的一个交点的横坐标在0与1之间,
对称轴在直线x=1右侧”的特点,而此时a=c,(其实a>c,a<c,a=c都有可能),故②错误;
∵-1<m<n<1,-2<m+n<2,
∴抛物线对称轴为:x=-![]() >1, -
>1, -![]() >2,m+n < -
>2,m+n < -![]() ,故③正确;
,故③正确;
当x=1时,a+b+c>0,2a+b>0,3a+2b+c>0,∴3a+c>-2b,∴-3a-c<2b,
∵a<0,b>0,c<0(图象与y轴交于负半轴),∴3|a|+|c|=-3a-c<2b=2|b|,故④正确.
故选A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】近视眼镜的度数y(度)与镜片焦距x(米)成反比例.已知200度的近视眼镜镜片的焦距为0.5米.求:
(1)y关于x的函数解析式;
(2)300度近视眼镜镜片的焦距.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4根小木棒,长度分别为3cm、5cm、7cm、9cm,任意取其中的3根小木棒首尾相接搭三角形,可搭出不同的三角形的个数为( )
A.5个
B.4个
C.3个
D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() ,其中
,其中![]() ,点A(-2,m)在该抛物线上,过点A作直线l∥x轴,与抛物线交于另一点B,与y轴交于点C.
,点A(-2,m)在该抛物线上,过点A作直线l∥x轴,与抛物线交于另一点B,与y轴交于点C.
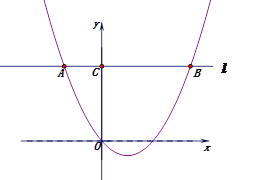
(1)求m的值.
(2)当a=2时,求点B的坐标.
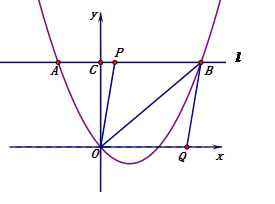
(3)如图2,以OB为对角线作菱形OPBQ,顶点P在直线l上,顶点Q在x轴上.
①若PB=2AP,求a的值.
②菱形OPBQ的面积的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台“走基层”栏目的一位记者乘汽车赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路,若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是
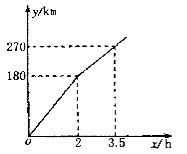
A. 汽车在高速公路上行驶速度为100km/h
B. 乡村公路总长为90km
C. 汽车在乡村公路上行驶速度为60km/h
D. 该记者在出发后4.5h到达采访地
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(![]() ,0)、(0,4),抛物线
,0)、(0,4),抛物线![]() 经过B点,且顶点在直线
经过B点,且顶点在直线![]() 上.
上.
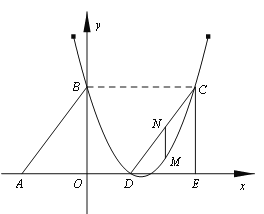
(1)求抛物线对应的函数关系式;
(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)若M点是CD所在直线下方该抛物线上的一个动点,过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为l.求l与t之间的函数关系式,并求l取最大值时,点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com