
����Ŀ����ͼ��Rt��ABO����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�OΪ����ԭ�㣬A��B���������ֱ�Ϊ��![]() ��0������0��4����������
��0������0��4����������![]() ����B�㣬�Ҷ�����ֱ��
����B�㣬�Ҷ�����ֱ��![]() �ϣ�
�ϣ�
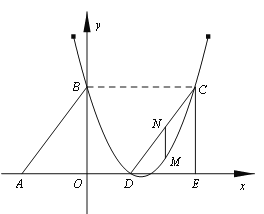
��1���������߶�Ӧ�ĺ�����ϵʽ��
��2������DCE������ABO��x������ƽ�Ƶõ��ģ����ı���ABCD������ʱ�����жϵ�C�͵�D�Ƿ��ڸ��������ϣ���˵�����ɣ�
��3����M����CD����ֱ���·����������ϵ�һ�����㣬����M��MNƽ����y�ύCD�ڵ�N�����M�ĺ�����Ϊt��MN�ij���Ϊl����l��t֮��ĺ�����ϵʽ������lȡ���ֵʱ����M�����꣮
���𰸡���1��![]()
��2���ڣ�������
��3��M��������![]() ��
�� ![]() ��
��
�������������������1����֪����������A��B��������Լ������ߵĶԳ��᷽�̣����ô���ϵ������������ߵĽ���ʽ��
��2���������AB�ij�����A��B����������ƽ��AB����λ�����ɵó�C��D�����꣬�ٴ��������ߵĽ���ʽ�н�����֤���ɣ�
��3������C��D�����꣬�����ֱ��CD�Ľ���ʽ����ô�߶�MN�ij�ʵ����ֱ��BC�������ߵĺ���ֵ�IJ�ɽ�x=t�������������Ľ���ʽ�У��ó���������ֵ�IJΪl�ı���ʽ���ɴ˿����l��t�ĺ�����ϵʽ���������ú��������ʼ������lȡ���ֵʱ����M�����꣮
�⣺��1����������y=![]() +bx+c�Ķ�����ֱ��x=�ϣ�
+bx+c�Ķ�����ֱ��x=�ϣ�
���������������߶�Ӧ�ĺ�����ϵʽΪy=![]() +m
+m
����B��0��4���ڴ��������ϣ�
��4=��![]() +m
+m
��m=��
����������ϵʽΪ��y=![]() ��=
��=![]() ��
��![]() x+4
x+4
��2����Rt��ABO��OA=3��OB=4��
��AB=![]() =5
=5
���ı���ABCD������
��BC=CD=DA=AB=5
��C��D���������ֱ��ǣ�5��4������2��0����
��x=5ʱ��y=��52��![]() ��5+4=4
��5+4=4
��x=2ʱ��y=��22��![]() ��2+4=0
��2+4=0
����C�͵�D�������������ϣ�
��3����ֱ��CD��Ӧ�ĺ�����ϵʽΪy=kx+b����
��![]() ��
��
��ã�![]() ��
��
��y=x��
��MN��y�ᣬM��ĺ�����Ϊt��
��N��ĺ�����ҲΪt��
��yM=![]() ��
��![]() t+4��yN=t����
t+4��yN=t����
��l=yN��yM=t������![]() ��
��![]() t+4��=��
t+4��=��![]() +
+![]() t��
t��![]() =��
=��![]() +
+
�ߩ���0��
����t=ʱ��l���=��yM=![]() ��
��![]() t+4=��
t+4=��
��ʱ��M������Ϊ��������


 ������ϵ�д�
������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��ͼ����ͼ��ʾ���������н��ۣ���2a+b��0��
��b��a��c������-1��m��n��1����m+n��![]() ����3|a|+|c|��2|b|��������ȷ�Ľ��۸����ǣ� ��
����3|a|+|c|��2|b|��������ȷ�Ľ��۸����ǣ� ��
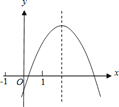
A. �٢ۢ� B. �٢� C. �٢� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���EΪ��BC����һ���㣬��AF��DE��DE��DC�ֱ���P��F�㣬��PC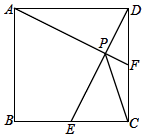
��1������EΪBC���е㣬��֤��F��ΪDC���е㣻
��2������EΪBC���е㣬PE=6��PC=4 ![]() ����PF�ij���
����PF�ij���
��3���������α߳�Ϊ4��ֱ��д��PC����Сֵ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������IJ����У���ɫ����ɫ����ɫ�IJ�������40��������ɫ��������ȫ��ͬ.С��ͨ���������������֣�����������ɫ����ɫ���Ƶ���ȶ���15%��45%���ڴ��а�ɫ��ܿ����ǣ� ��.
A.6��B.16��C.18��D.24��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������������Ϸ����һ�����������������20��ֽ������������ĸ��������ͬ��������12��ֽ������ĸΪA��8��ֽ���ϵ���ĸΪB����ֽ��ҡ�Ⱥ���������һ�ţ��������ֽ���ϵ���ĸΪA����С��ʤ���������ֽ���ϵ���ĸΪB��������ʤ��
��1�������Ϸ��ƽ����˵�����ɣ�
��2�����������������ٷ���3����ǰ����ͬ��ֽ����������ĸΪB����ʱ�����Ϸ��˭������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ����x�ύ�ڵ�A����1��0�����Գ���Ϊֱ��x=1����y��Ľ���B�ڣ�0��2���ͣ�0��3��֮�䣨���������㣩�����н��ۣ��ٵ�x��3ʱ��y��0����3a+b��0���۩�1��a�ܩ�![]() ����4ac��b2��8a��������ȷ�Ľ����ǣ� ����
����4ac��b2��8a��������ȷ�Ľ����ǣ� ����
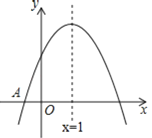
A. �٢ڢ� B. �٢ڢ� C. �٢ۢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ�깺������Ϊ15Ԫͯװ���ɼ�������һ��ʱ����֣������ۼ�Ϊ25Ԫʱƽ��ÿ�����۳�8�����������ۼ�ÿ����2Ԫ��ƽ��ÿ���ܶ��۳�4������ÿ���Ķ���Ϊ Ԫʱ���÷�װ��ƽ��ÿ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ѿ���Խ�˺����������Ϊ�����й��˴���ǰ���ͷ���С���������������罻����Ҫ���壬2019���Ϧ�������ڼ䣬����8.23���˴��շ��ź��ͬ������7.12%���ÿ�ѧ��������ʾ8.23�������Ϊ��������
A.8.23��107B.8.23��108C.8.23��109D.0.83��109
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com