
【题目】如图,在正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 上的一点,点
上的一点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
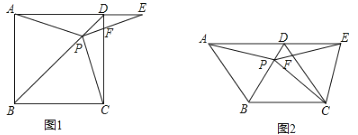
(1)证明:![]() ;
;
(2)如图,把正方形![]() 改为菱形
改为菱形![]() ,其它条件不变,当
,其它条件不变,当![]() 时,连接
时,连接![]() ,试探究线段
,试探究线段![]() 与线段
与线段![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)证明见解析;(2)AP=CE,理由见解析.
【解析】
(1)先证出△ABP≌△CBP,得PA=PC,由于PA=PE,得PC=PE;
(2)根据已知和(1)易证△ADP≌△CDP,得PC=PE,∠DAP=∠DCP,由PA=PE,得到∠DAP=∠AEP,∠DCP=∠E,而![]() 可得∠CDE=60°,再结合三角形内角和定理可得∠EPC=60°,△EPC为等边三角形,即可得到结论;
可得∠CDE=60°,再结合三角形内角和定理可得∠EPC=60°,△EPC为等边三角形,即可得到结论;
解:(1)证明:在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,
∵PB=PB,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)解:AP=CE;
理由如下:
在菱形ABCD中,AD=DC,∠ADP=∠CDP=60°,
∵PD=PD,
∴△ADP≌△CDP(SAS),
∴PA=PC,∠DAP=∠DCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DEP,
∴∠DCP=∠DEP
∵∠CFP=∠EFD
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠DEP,
即∠CPE=∠CDE=180°﹣∠ADC=180°﹣120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴ AP=CE.


科目:初中数学 来源: 题型:
【题目】下表显示了同学们用计算机模拟随机投针实验的某次实验的结果.
投针次数n | 1000 | 2000 | 3000 | 4000 | 5000 | 10000 | 20000 |
针与直线相交的次数m | 454 | 970 | 1430 | 1912 | 2386 | 4769 | 9548 |
针与直线相交的频率p=
| 0.454 | 0.485 | 0.4767 | 0.478 | 0.4772 | 0.4769 | 0.4774 |
下面有三个推断:
①投掷1000次时,针与直线相交的次数是454,针与直线相交的概率是0.454;
②随着实验次数的增加,针与直线相交的频率总在0.477附近,显示出一定的稳定性,可以估计针与直线相交的概率是0.477;
③若再次用计算机模拟此实验,则当投掷次数为10000时,针与直线相交的频率一定是0.4769.
其中合理的推断的序号是:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
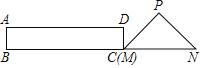
【题目】如图,在Rt△PMN中,∠P=90°,PM=PN,MN=6cm,矩形ABCD中AB=2cm,BC=10cm,点C和点M重合,点B、C(M)、N在同一直线上,令Rt△PMN不动,矩形ABCD沿MN所在直线以每秒1cm的速度向右移动,至点C与点N重合为止,设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y,则y与x的大致图象是( )
A. 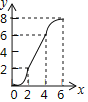 B.
B. 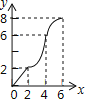 C.
C. 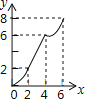 D.
D. 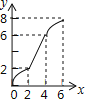
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+3的图象经过A(﹣1,0)、C(3,0)、并且与y轴相交于点B,点P是直线BC上方的抛物线上的一动点,PQ∥y轴交直线BC于点Q.
(1)求此二次函数的表达式;
(2)求线段PQ的最大值;
(3)在抛物线的对称轴上,是否存在点M,使△MAB为等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
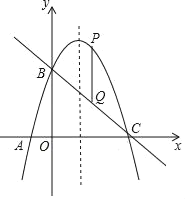
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,高度相同的两根电线杆AB、CD均垂直于地面AF,某时刻电线杆AB的影子为地面上的线段AE,电线杆CD的影子为地面上的线段CF和坡面上的线段FG.已知坡面FG的坡比i=1:0.75,又AE=6米,CF=1米,FG=5米,那么电线杆AB的高度为______米.
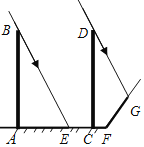
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军自制的匀速直线运动遥控车模型甲、乙两车同时分别从![]() 、
、![]() 出发,沿直线轨道同时到达
出发,沿直线轨道同时到达![]() 处,已知乙的速度是甲的速度的1.5倍,甲、乙两遥控车与
处,已知乙的速度是甲的速度的1.5倍,甲、乙两遥控车与![]() 处的距离
处的距离![]() 、
、![]() (米)与时间
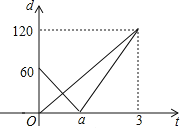
(米)与时间![]() (分钟)的函数关系如图所示,则下列结论中:①
(分钟)的函数关系如图所示,则下列结论中:①![]() 的距离为120米;②乙的速度为60米/分;③
的距离为120米;②乙的速度为60米/分;③![]() 的值为
的值为![]() ;④若甲、乙两遥控车的距离不少于10米时,两车信号不会产生互相干扰,则两车信号不会产生互相干扰的
;④若甲、乙两遥控车的距离不少于10米时,两车信号不会产生互相干扰,则两车信号不会产生互相干扰的![]() 的取值范围是
的取值范围是![]() ,其中正确的有( )个
,其中正确的有( )个
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)、(﹣2,1),将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),则点A1,C1的坐标分别是 ( )

A. A1(4,4),C1(3,2) B. A1(3,3),C1(2,1)
C. A1(4,3),C1(2,3) D. A1(3,4),C1(2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]() ,当
,当![]() 时,函数有最大值
时,函数有最大值![]() .
.
(1)求此二次函数图象与坐标轴的交点;
(2)将函数![]() 图象
图象![]() 轴下方部分沿
轴下方部分沿![]() 轴向上翻折,得到的新图象,若点
轴向上翻折,得到的新图象,若点![]() 是翻折得到的抛物线弧部分上任意一点,若关于
是翻折得到的抛物线弧部分上任意一点,若关于![]() 的一元二次方程
的一元二次方程![]() 恒有实数根时,求实数
恒有实数根时,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com